
【题目】如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.
(1)请直接写出∠AEB的度数,∠AEB= ;
(2)将△AED沿直线AD向上翻折,得△AFD.求证:四边形AEDF是菱形;
(3)连接EF,交AD于点 O,试求EF的长?
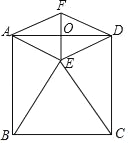
【答案】(1)75°;(2)证明见解析;(3)![]()
【解析】
试题(1)由正方形和等边三角形的性质得出∠ABE=30°,AB=BE,由等腰三角形的性质和三角形内角和定理即可求出∠AEB的度数;
(2)先判断出△ABE≌△DCE,得到AE=ED,再由翻折的性质即可得出结论;
(3)先由等边三角形的性质求出EH,进而得出OE,借助(2)的结论即可求出EF.
试题解析:(1)∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∵△EBC是等边三角形,
∴BE=BC,∠EBC=60°,
∴∠ABE=90°-60°=30°,AB=BE,
∴∠AEB=∠BAE=![]() (180°-30°)=75°;
(180°-30°)=75°;
(2)∵四边形ABCD为正方形,
∴∠ABC=∠BCD=90°,AB=CD,
∵△BCE为等边三角形,
∴∠BCE=∠EBC=60°,BE=EC,
∴∠ABE=∠DCE=90°-60°=30°,
∴△ABE≌△DCE,
∴AE=ED,
∵△AED沿着AD翻折为△AFD,
∴AE=ED=AF=FD,
∴四边形AEDF是菱形;
(3)如图,
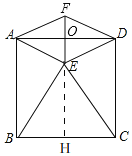
由翻折知,AE=AF,∠FAO=∠EAO,
∴EF⊥AD,过点E作EH⊥BC于H,
在等边三角形BCE中,BC=2,
∴EH=![]() BC=
BC=![]() ,
,
∴EO=OH-EH=AB-EH=2-![]() ,
,
∴EF=2EO=2(2-![]() )=4-2
)=4-2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
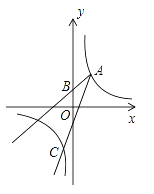
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )
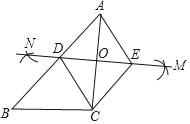
A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:
(1)若小明随机选择一个插座插入,则插入A的概率为 ;
(2)现小明对手机和学习机两种电器充电,请用列表或画树状图的方法表示出两个插头插入插座的所有可能情况,并计算两个插头插在相邻插座的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张面积为100cm2的正方形纸片,其正投影的面积可能是100cm2吗?可能是80cm2吗?可能是120cm2吗?试确定这张正方形纸片的正投影面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() ,射线
,射线![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,设点
的速度运动,设点![]() 运动的时间为
运动的时间为![]() .
.
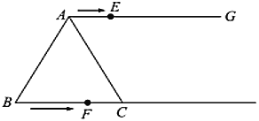
(1)当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() _________
_________![]() ,当点
,当点![]() 在线段
在线段![]() 的延长线上运动时,
的延长线上运动时,![]() _________
_________![]() (请用含
(请用含![]() 的式子表示);
的式子表示);
(2)在整个运动过程中,当以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() 的值;
的值;
(3)求当![]() _________时,
_________时,![]() ,
,![]() 两点间的距离最小.
两点间的距离最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
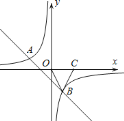
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
![]() Ⅰ
Ⅰ![]() 试确定上述反比例函数和一次函数的表达式;
试确定上述反比例函数和一次函数的表达式;
![]() Ⅱ
Ⅱ![]() 连OB,在x轴上取点C,使
连OB,在x轴上取点C,使![]() ,并求
,并求![]() 的面积;
的面积;
![]() Ⅲ
Ⅲ![]() 直接写出一次函数值大于反比例函数值的自变量x的取值范围.
直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com