
【题目】如图,把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,若直线DF垂直平分AB,垂足为点E,连接BF,CE,且BC=2.下面四个结论:

①BF=![]() ;
;
②∠CBF=45°;
③∠CED=30°;
④△ECD的面积为![]() ,
,
其中正确的结论有_____.(填番号)
【答案】①②④
【解析】
利用旋转的性质得CF=CB=2,∠BCF=90°,则可得△CBF为等腰直角三角形,于是可对①②进行判断;由于直线DF垂直平分AB,则FA=FB,BE=AE,于是根据等腰三角形的性质和三角形外角性质可计算出∠ECA=∠A=22.5°,然后根据三角形内角和可计算出∠CEF,从而可对③进行判断;作EH⊥BD于H,如图,根据三角形中位线性质得EH=![]() AC=
AC=![]() +1,利用旋转性质得CD=CA=2+2
+1,利用旋转性质得CD=CA=2+2![]() ,则利用三角形面积公式可计算出△ECD的面积,从而可对④进行判断.
,则利用三角形面积公式可计算出△ECD的面积,从而可对④进行判断.
∵把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,
∴CF=CB=2,∠BCF=90°,
∴△CBF为等腰直角三角形,
∴BF=![]() BC=2
BC=2![]() ,∠CBF=45°,所以①②正确;
,∠CBF=45°,所以①②正确;
∵直线DF垂直平分AB,
∴FA=FB,BE=AE,
∴∠A=∠ABF,
而∠BFC=∠A+∠ABF=45°,
∴∠A=22.5°,
∵CE为斜边AB上的中线,
∴EC=EA,
∴∠ECA=∠A=22.5°,
∴∠CEF=180°﹣90°﹣2×22.5°=45°,所以③错误;
作EH⊥BD于H,如图,
∵把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,
∴CD=CA=2+2![]() ,
,
∵点E为AB的中点,
∴EH=![]() AC=
AC=![]() +1,
+1,
∴△ECD的面积=![]() (
(![]() +1)(2+2
+1)(2+2![]() )=2
)=2![]() +3,所以④正确.
+3,所以④正确.
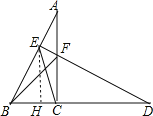
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我把对角线互相垂直的四边形叫做“垂美四边形”.
(1)性质探究:如图1.已知四边形ABCD中,AC⊥BD,垂足为O,求证:AB2+CD2=AD2+BC2.
(2)解决问题:已知AB=5,BC=4,分别以△ABC的边BC和AB向外作等腰Rt△BCQ和等腰Rt△ABP.
①如图2,当∠ACB=90°,连接PQ,求PQ;
②如图3,当∠ACB≠90°,点M、N分别是AC、AP中点连接MN.若MN=![]() ,则S△ABC= .
,则S△ABC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条笔直跑道上的A,B两处相距500米,甲从A处,乙从B处,两人同时相向匀速而跑,直到乙到达A处时停止,且甲的速度比乙大.甲、乙到A处的距离![]() (米)与跑动时间
(米)与跑动时间![]() (秒)的函数关系如图14所示.
(秒)的函数关系如图14所示.
(1)若点M的坐标(100,0),求乙从B处跑到A处的过程中![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若两人之间的距离不超过200米的时间持续了40秒.
①当![]() 时,两人相距200米,请在图14中画出P(
时,两人相距200米,请在图14中画出P(![]() ,0).保留画图痕迹,并写出画图步骤;
,0).保留画图痕迹,并写出画图步骤;
②请判断起跑后![]() 分钟,两人之间的距离能否超过420米,并说明理由.
分钟,两人之间的距离能否超过420米,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)求证:BM=CN;
(2)若AB=8,AC=4,求BM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是人字型金属屋架的示意图,该屋架由BC、AC、BA、AD四段金属材料焊接而成,其中A、B、C、D四点均为焊接点,且AB=AC,D为BC的中点,假设焊接所需的四段金属材料已截好,并已标出BC段的中点D,那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及焊接点是( )
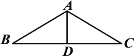
A.AB和AD,点AB.AB和AC,点B
C.AC和BC, 点CD.AD和BC,点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y = x2 - 4x + 3.
(1)用配方法将y = x2 - 4x + 3化成y = a(x - h)2 + k的形式;
(2)在平面直角坐标系![]() 中画出该函数的图象;
中画出该函数的图象;
(3)当0≤x≤3时,y的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,点
中,点![]() 为
为![]() 边中点,点
边中点,点![]() 为
为![]() 边中点;点
边中点;点![]() ,
, ![]() 为
为![]() 边三等分点,
边三等分点, ![]() ,
, ![]() 为
为![]() 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形
边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形![]() 的面积与图3中四边形
的面积与图3中四边形![]() 的面积相等吗?
的面积相等吗?
(1)小瑞的探究过程如下
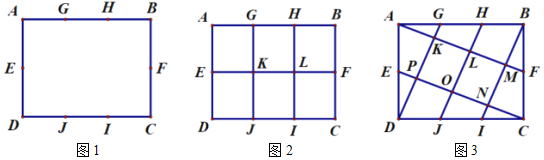
在图2中,小瑞发现, ![]() ;
;
在图3中,小瑞对四边形![]() 面积的探究如下. 请你将小瑞的思路填写完整:
面积的探究如下. 请你将小瑞的思路填写完整:
设![]() ,
, ![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
又∵![]() ,
, ![]()
∴![]()
∴![]() ,
, ![]() ,
, ![]()
∴![]() ,则
,则![]() (填写“
(填写“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
(2)小瑞又按照图4的方式连接矩形![]() 对边上的点.则
对边上的点.则![]() .
.
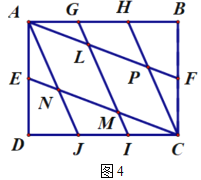
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com