
【题目】如图1,在矩形![]() 中,点
中,点![]() 为
为![]() 边中点,点
边中点,点![]() 为
为![]() 边中点;点
边中点;点![]() ,
, ![]() 为
为![]() 边三等分点,
边三等分点, ![]() ,
, ![]() 为
为![]() 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形
边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形![]() 的面积与图3中四边形
的面积与图3中四边形![]() 的面积相等吗?
的面积相等吗?
(1)小瑞的探究过程如下
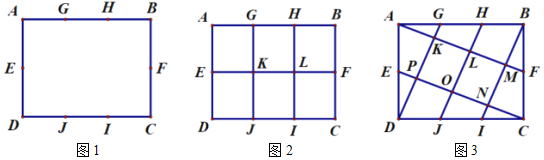
在图2中,小瑞发现, ![]() ;
;
在图3中,小瑞对四边形![]() 面积的探究如下. 请你将小瑞的思路填写完整:
面积的探究如下. 请你将小瑞的思路填写完整:
设![]() ,
, ![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
又∵![]() ,
, ![]()
∴![]()
∴![]() ,
, ![]() ,
, ![]()
∴![]() ,则
,则![]() (填写“
(填写“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
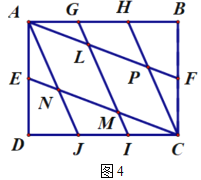
(2)小瑞又按照图4的方式连接矩形![]() 对边上的点.则
对边上的点.则![]() .
.
【答案】答案见解析.
【解析】试题分析:(1)由六个小长方形的面积相等,得到![]() .设
.设![]() ,
, ![]() .由相似三角形的性质得到:
.由相似三角形的性质得到: ![]() ,
, ![]() .再由
.再由![]() ,
, ![]() ,得到a=
,得到a= ![]() ,
, ![]() =42b,
=42b, ![]() =6b,即可得出结论;
=6b,即可得出结论;
(2)连接DN.设![]() =a,
=a, ![]() =b,则S△EDN=b,S△NJC=4a,S△DNJ=
=b,则S△EDN=b,S△NJC=4a,S△DNJ=![]() S△NJC =2a.由S△ADJ=
S△NJC =2a.由S△ADJ=![]() SABCD,S△CDE=
SABCD,S△CDE=![]() SABCD,得到:b=1.5a,b=
SABCD,得到:b=1.5a,b=![]() SABCD.由S△CFP=S△AEN, SAECF=
SABCD.由S△CFP=S△AEN, SAECF=![]() SABCD, SANML=SMCPL即可得到结论.
SABCD, SANML=SMCPL即可得到结论.
试题解析:解:(1) ∵六个小长方形的面积相等,∴![]() .
.
设![]() ,
, ![]() .∵EC∥AF,∴△DEP∽△DAK,且相似比为1:2,得到
.∵EC∥AF,∴△DEP∽△DAK,且相似比为1:2,得到![]() .∵GD∥BI,∴△AGK∽△ABM,且相似比为1:3,得到
.∵GD∥BI,∴△AGK∽△ABM,且相似比为1:3,得到![]() .又∵
.又∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∴a= ![]() ,
, ![]() =42b,
=42b, ![]() =6b,∴
=6b,∴![]() ,则
,则![]() ;
;
(2)连接DN.设![]() =a,
=a, ![]() =b,则S△EDN=b,S△NJC=4a,S△DNJ=
=b,则S△EDN=b,S△NJC=4a,S△DNJ=![]() S△NJC =2a.∵S△ADJ=
S△NJC =2a.∵S△ADJ=![]() SABCD,S△CDE=
SABCD,S△CDE=![]() SABCD,∴2b+2a=
SABCD,∴2b+2a=![]() SABCD,b+6a=
SABCD,b+6a=![]() SABCD, 解得:b=1.5a,b=
SABCD, 解得:b=1.5a,b=![]() SABCD.∵S△CFP=S△AEN, SAECF=
SABCD.∵S△CFP=S△AEN, SAECF=![]() SABCD,∴SANML=SMCPL=(
SABCD,∴SANML=SMCPL=(![]() SABCD-2×
SABCD-2×![]() SABCD)×
SABCD)×![]() =
=![]()
![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,若直线DF垂直平分AB,垂足为点E,连接BF,CE,且BC=2.下面四个结论:

①BF=![]() ;
;
②∠CBF=45°;
③∠CED=30°;
④△ECD的面积为![]() ,
,
其中正确的结论有_____.(填番号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距360千米,一辆贩毒车从甲地往乙地接头取货,警方截取情报后,立即组织干警从甲地出发,前往乙地缉拿这伙犯罪分子,结果警车与贩毒车同时到达,将犯罪分子一网打尽.已知贩毒车比警车早出发1小时15分,警车与贩毒车的速度比为4∶3,求贩毒车和警车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
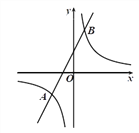
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 与反比例函数
与反比例函数![]() 交于点
交于点![]() ,
, ![]() .
.
(1)分别求出反比例函数和一次函数的表达式;
(2)根据函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒3°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,直线MN保持不动,如图2,设旋转时间为t(0≤t≤60,单位秒)

(1)当t=2时,求∠AOB的度数;
(2)在运动过程中,当∠AOB第二次达到63°时,求t的值;
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而小于180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
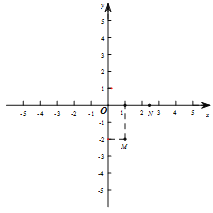
【题目】已知抛物线![]() (
(![]() 为任意实数)经过下图中两点M(1,-2)、N(
为任意实数)经过下图中两点M(1,-2)、N(![]() ,0),其中M为抛物线的顶点,N为定点.下列结论:
,0),其中M为抛物线的顶点,N为定点.下列结论:
①若方程![]() 的两根为
的两根为![]() ,
, ![]() (
(![]() ),则
),则![]() ,
, ![]() ;
;
②当![]() 时,函数值
时,函数值![]() 随自变量
随自变量![]() 的减小而减小.
的减小而减小.
③![]() ,
, ![]() ,
, ![]() .
.
④垂直于![]() 轴的直线与抛物线交于C、D两点,其C、D两点的横坐标分别为
轴的直线与抛物线交于C、D两点,其C、D两点的横坐标分别为![]() 、
、![]() ,则
,则![]() =2 .
=2 .
其中正确的是( )
A. ①② B. ①④ C. ②③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com