
【题目】如图,点![]() 在⊙
在⊙![]() 的直径
的直径![]() 的延长线上,点
的延长线上,点![]() 在⊙
在⊙![]() 上,
上, ![]() ,
, ![]() .
.
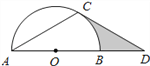
(1)求证: ![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若⊙![]() 的半径为
的半径为![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)连接OC.只需证明∠OCD=90°.根据等腰三角形的性质即可证明;
(2)先根据直角三角形中30°的锐角所对的直角边是斜边的一半求出OD,然后根据勾股定理求出CD,则阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积.
(1)证明:连接OC.

∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=∠ACD-∠2=90°,
即OC⊥CD,
∴CD是⊙O的切线;
(2)解:∠1=∠2+∠A=60°.
∴S扇形BOC=![]() =
=![]() .
.
在Rt△OCD中,∠D=30°,
∴OD=2OC=4,
∴CD=![]() =
=![]() .
.
∴SRt△OCD=![]() OC×CD=
OC×CD=![]() ×2×
×2×![]() =
=![]() .
.
∴图中阴影部分的面积为: ![]() -
-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是人字型金属屋架的示意图,该屋架由BC、AC、BA、AD四段金属材料焊接而成,其中A、B、C、D四点均为焊接点,且AB=AC,D为BC的中点,假设焊接所需的四段金属材料已截好,并已标出BC段的中点D,那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及焊接点是( )
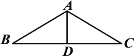
A.AB和AD,点AB.AB和AC,点B
C.AC和BC, 点CD.AD和BC,点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,点
中,点![]() 为
为![]() 边中点,点
边中点,点![]() 为
为![]() 边中点;点
边中点;点![]() ,
, ![]() 为
为![]() 边三等分点,
边三等分点, ![]() ,
, ![]() 为
为![]() 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形
边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形![]() 的面积与图3中四边形
的面积与图3中四边形![]() 的面积相等吗?
的面积相等吗?
(1)小瑞的探究过程如下
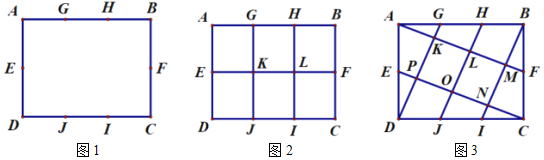
在图2中,小瑞发现, ![]() ;
;
在图3中,小瑞对四边形![]() 面积的探究如下. 请你将小瑞的思路填写完整:
面积的探究如下. 请你将小瑞的思路填写完整:
设![]() ,
, ![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
又∵![]() ,
, ![]()
∴![]()
∴![]() ,
, ![]() ,
, ![]()
∴![]() ,则
,则![]() (填写“
(填写“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
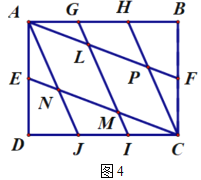
(2)小瑞又按照图4的方式连接矩形![]() 对边上的点.则
对边上的点.则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 垂直平分线段
垂直平分线段![]() (
(![]() ),点
),点![]() 是线段
是线段![]() 延长线上的一点,且
延长线上的一点,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 的延长线与点
的延长线与点![]() .
.

(1)若![]() ,则
,则![]() ______(用
______(用![]() 的代数式表示);
的代数式表示);
(2)线段![]() 与线段
与线段![]() 相等吗?为什么?
相等吗?为什么?
(3)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 |
|
|
| … |
我们把某格中字母和所得到的多项式称为“特征多项式”,例如第1格的“特征多项式”为![]() .
.
回答下列问题:
(1)第3格的“特征多项式”为____________,
第4格的“特征多项式”为____________,
第![]() 格的“特征多项式”为____________;
格的“特征多项式”为____________;
(2)若第1格的“特征多项式”的值为10,第2格的“特征多项式”的值为19,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2019按照一定规律排成下表:

记aij表示第i行第j个数,如a14=4表示第1行第4个数是4.
(1)直接写出a42= ,a53= ;
(2)①如果aij=2019,那么i= ,j= ;②用i,j表示aij= ;
(3)将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2027.若能,求出这5个数中的最小数,若不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0.
(1)求点C表示的数;
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,若AP+BQ=2PQ,求时间t;
(3)若点P从A向右运动,点M为AP中点,在P点到达点B之前:①![]() 的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
(1)当⊙O的半径为1时:
①点![]() ,
, ![]() ,
, ![]() 中,⊙O的关联点有_____________________.
中,⊙O的关联点有_____________________.
②直线经过(0,1)点,且与![]() 轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标
轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标![]() 的取值范围.
的取值范围.
(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com