
【题目】如图所示,矩形ABCD的面积为128cm2 , 它的两条对角线交于点O1 , 以AB、AO1为两边邻作平行四边形ABC1O1 , 平行四边形ABC1O1的对角线交于点O2 , 同样以AB、AO2为两邻边作平行四边形ABC2O2 , …,依此类推,则平行四边形ABC7O7的面积为 . 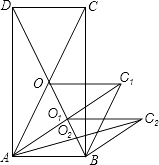
【答案】![]()
【解析】解:根据矩形的对角线相等且互相平分,
平行四边形ABC1O1底边AB上的高为 ![]() BC,
BC,
平行四边形ABC2O2底边AB山的高为 ![]() ×
× ![]() BC=(
BC=( ![]() )2BC,
)2BC,
所以平行四边形ABCnOn底边AB上的高为×( ![]() )nBC,
)nBC,
∵S矩形ABCD=ABBC=128,
∴S平行四边形ABCnOn=AB×( ![]() )nBC=128×(
)nBC=128×( ![]() )n ,
)n ,
∴当n=7时,平行四边形ABC7O7的面积为=128×( ![]() )7 ,
)7 ,
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用平行四边形的性质和矩形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;矩形的四个角都是直角,矩形的对角线相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC= ![]() b2+
b2+ ![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB= ![]() c2+
c2+ ![]() a(b﹣a)
a(b﹣a)
∴ ![]() b2+
b2+ ![]() ab=
ab= ![]() c2+
c2+ ![]() a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 . 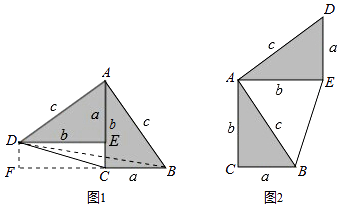
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值______________.
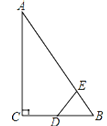
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作
法和证明);
(2)连接DE,求证:△ADE≌△BDE。
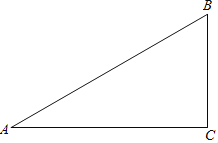
查看答案和解析>>
科目:初中数学 来源: 题型:
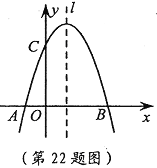
【题目】(本题10分)如图,已知抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C,点B的坐标为(3,0)。
轴交于点C,点B的坐标为(3,0)。
(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴![]() 上的一个动点,当PA+PC的值最小时,求点P的坐标。
上的一个动点,当PA+PC的值最小时,求点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com