
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC= ![]() b2+
b2+ ![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB= ![]() c2+
c2+ ![]() a(b﹣a)
a(b﹣a)
∴ ![]() b2+
b2+ ![]() ab=
ab= ![]() c2+
c2+ ![]() a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 . 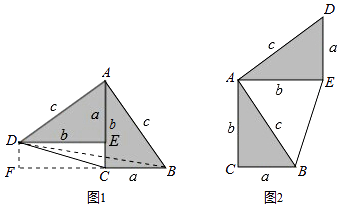
科目:初中数学 来源: 题型:
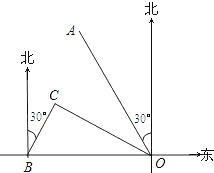
【题目】如图,港口B位于港口O正西方向120海里处,小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏西30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去.
(1)快艇从港口B到小岛C需要多少时间?
(2)快艇从小岛C出发后最少需要多少时间才能和考察船相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°. 求小岛B到河边公路AD的距离.
(参考数据:sin37°≈ 0.60,cos37° ≈ 0.80,tan37° ≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
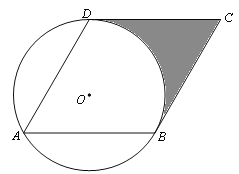
【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的原点为0,点A、B、C是数轴上的三点,点B对应的数位1,AB=6,BC=2,动点P、Q同时从A、C出发,分别以每秒2个长度单位和每秒1个长度单位的速度沿数轴正方向运动.设运动时间为t秒(t>0) ![]()
(1)求点A、C分别对应的数;
(2)求点P、Q分别对应的数(用含t的式子表示)
(3)试问当t为何值时,OP=OQ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD的面积为128cm2 , 它的两条对角线交于点O1 , 以AB、AO1为两边邻作平行四边形ABC1O1 , 平行四边形ABC1O1的对角线交于点O2 , 同样以AB、AO2为两邻边作平行四边形ABC2O2 , …,依此类推,则平行四边形ABC7O7的面积为 . 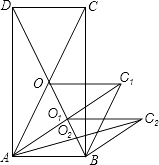
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农民张大伯因病住院,手术费为a元,其它费用为b元.由于参加农村合作医疗,
手术费报销85%,其它费用报销60%,则张大伯此次住院可报销 ▲ 元.(用代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com