
已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.

(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
(1)点P的坐标为(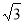 ,3).
,3).
(2)抛物线的解析式为y=﹣x2+6
(3)点A、B、C、D围成的多边形的面积为4+2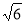 或6
或6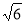 .
.
【解析】
试题分析:(1)由切线的性质可得∠MPO=90°,由勾股定理可求出PO,由三角形PMO的面积利用面积法可求出PK,然后再运用勾股定理可求出OK,就可得到点P的坐标.
(2)可设顶点为(0,6)的抛物线的解析式为y=ax2+6,然后将点P的坐标代入就可求出抛物线的解析式.
(3)直线y=m与⊙M相切有两种可能,只需对这两种情况分别讨论就可求出对应多边形的面积.
试题解析:(1)如图1,
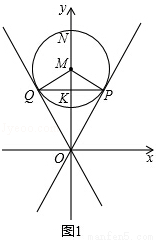
∵⊙M与OP相切于点P,
∴MP⊥OP,即∠MPO=90°.
∵点M(0,4)即OM=4,MP=2,
∴OP=2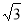 .
.
∵⊙M与OP相切于点P,⊙M与OQ相切于点Q,
∴OQ=OP,∠POK=∠QOK.
∴OK⊥PQ,QK=PK.
∴PK=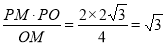 .
.
∴OK=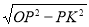 =3.
=3.
∴点P的坐标为(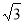 ,3).
,3).
(2)如图2,
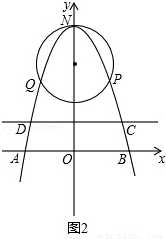
设顶点为(0,6)的抛物线的解析式为y=ax2+6,
∵点P(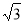 ,3)在抛物线y=ax2+6上,
,3)在抛物线y=ax2+6上,
∴3a+6=3.
解得:a=﹣1.
则该抛物线的解析式为y=﹣x2+6.
(3)当直线y=m与⊙M相切时,
则有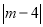 =2.
=2.
解得;m1=2,m2=6.
①m=2时,如图3,

则有OH=2.
当y=2时,解方程﹣x2+6=2得:x=±2,
则点C(2,2),D(﹣2,2),CD=4.
同理可得:AB=2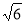 .
.
则S梯形ABCD=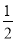 (DC+AB)•OH=
(DC+AB)•OH=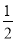 ×(4+2
×(4+2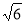 )×2=4+2
)×2=4+2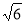 .
.
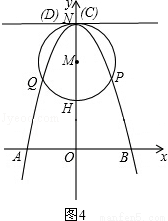
②m=6时,如图4,
此时点C、点D与点N重合.
S△ABC=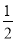 AB•OC=
AB•OC=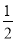 ×2
×2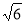 ×6=6
×6=6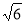 .
.
综上所述:点A、B、C、D围成的多边形的面积为4+2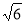 或6
或6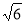 .
.
考点:1、解一元二次方程;2、待定系数法求二次函数解析式;3、勾股定理;4、切线长定理.


科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:填空题
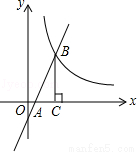
如图,一次函数y=kx﹣1的图象与x轴交于点A,与反比例函数 (x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是 .
(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:选择题
张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子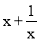 (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是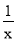 ,矩形的周长是2(
,矩形的周长是2(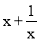 );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x=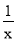 (x>0),解得x=1,这时矩形的周长2(
(x>0),解得x=1,这时矩形的周长2(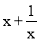 )=4最小,因此
)=4最小,因此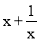 (x>0)的最小值是2.模仿张华的推导,你求得式子
(x>0)的最小值是2.模仿张华的推导,你求得式子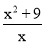 (x>0)的最小值是( )
(x>0)的最小值是( )
A.2 B.1 C.6 D.10
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:选择题
A、B、C、D四名选手参加50米决赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若A首先抽签,则A抽到1号跑道的概率是( )
A.1 B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西百色卷)数学(解析版) 题型:解答题
如图,在边为的1正方形组成的网格中,建立平面直角坐标系,若A(﹣4,2)、B(﹣2,3)、C(﹣1,1),将△ABC沿着x轴翻折后,得到△DEF,点B的对称点是点E,求过点E的反比例函数解析式,并写出第三象限内该反比例函数图象所经过的所有格点的坐标.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西百色卷)数学(解析版) 题型:填空题
已知甲、乙两组抽样数据的方差:S =95.43,S
=95.43,S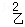 =5.32,可估计总体数据比较稳定的是 组数据.
=5.32,可估计总体数据比较稳定的是 组数据.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西河池卷)数学(解析版) 题型:解答题
某县为了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘成如下的频数分布表和频数分布直方图(未完成):

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第 组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为 ;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为 人.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西桂林卷)数学(解析版) 题型:选择题
两圆的半径分别为2和3,圆心距为7,则这两圆的位置关系为( )
A.外离 B.外切 C.相交 D.内切
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com