
��ͼ1���ھ���ABCD�У�AB��4��AD��2����P�DZ�AB�ϵ�һ������(�����A����B�غ�)����Q�ڱ�AD�ϣ�����CBP����QAP�ֱ���PC��PQ�۵���ʹB����E���غϣ�A����F���غϣ���P��E��F���㹲�ߣ�
��1������Eƽ���߶�PF�����ʱAQ�ij�Ϊ���٣�
��2�����߶�CE���߶�QF���ڵ�ƽ��ֱ��֮��ľ���Ϊ2�����ʱAP�ij�Ϊ���٣�
��3���ڡ��߶�CE�������߶�QF��������A���������У��Ƿ����������ͬһ��ֱ���ϵ�����������ڣ������ʱAP�ij����������ڣ���˵�����ɣ�


��1��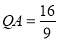 ��
��
��2��AP�ij�Ϊ1��3��
��3����CE���A��ͬһֱ���ϣ�AP=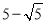 ����CE��QF��ͬһֱ���ϣ�AP=2��
����CE��QF��ͬһֱ���ϣ�AP=2��
��������
�����������1���Ȼ���ʾ��ͼ�����۵�֪����AQP�ա�FQP����CPB�ա�CPE����������AB�ߵĹ�ϵ֪����Eƽ��FP����BP=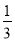 AB��AP=
AB��AP=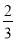 AB������֪������CP��QP������QAP�ס�PBC�����ɱ�֮��ijɱ����ù���AQ�ķ��̣��������;
AB������֪������CP��QP������QAP�ס�PBC�����ɱ�֮��ijɱ����ù���AQ�ķ��̣��������;
��2���ɣ�1����EP=BP��FP=AP��PB+AP=10���߶�CE���߶�QF���ڵ�ƽ��ֱ��֮��ľ���Ϊ2���ʾEF=2���������ֿ��ܣ�PF=EP+2��EP=FP+2�����ǵõ�������ϵʽ���ý���;
��3�����߶�CE�������߶�QF��������A�������ߣ�˼����P�˶�����ֽ�ص㣬QF������A���ߣ���CE��QF����ʱ��P��ǡΪAB�е㣬��ͼ�����߶ζ���CD�ϣ���CE��A����ʱ�������ӶԽ���AC��CE��AC�ϣ���ʱ��AEP�ס�ABC������AP�ij�����
�����������1������CBP����QAP�ֱ���PC��PQ�۵����õ���QFP����PCE������AQP�ա�FQP����CPB�ա�CPE
��PA=PF��PB=PE����QPA=��QPF����CPB=��CPE��
��EF=EP��
��AB=AP+PB=FP+PB=EF+EP+PB=3PB��
��AB=4��
��PB=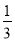 AB =
AB =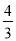 ��
��
��AP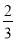 AB =
AB =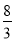 ��
��
��180��=��QPA+��QPF+��CPB+��CPE=2����QPA+��CPB����
���QPA+��CPB=90�㣮
���ı���ABCD�Ǿ��Σ�
���A=��B=90�㣬
���CPB+��PCB=90�㣬
���QPA=��PCB��
���QAP�ס�PBC��
��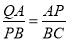 ��
��
��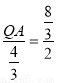 ��
��
��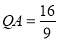 ��
��
��2�������⣬��PF=EP+2��EP=FP+2��
��EP��PF=2ʱ��
��EP=PB��PF=AP��
��PB��AP=2��
��AP+PB=4��
��2BP=6��
��BP=3��
��AP=1��
��PF��EP=2ʱ��
��EP=PB��PF=AP��
��AP��PB=2��
��AP+PB=4��
��2AP=6��
��AP=3��
��AP�ij�Ϊ1��3��
��3������CE���A��ͬһֱ���ϣ���ͼ2������AC����E��AC�ϣ�
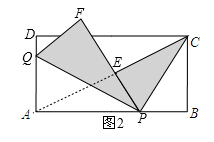
����AEP����ABC��
��APE=��B=90�㣬��EAP=��BAC��
���AEP�ס�ABC��
��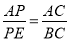 ��
��
��AP=x����EP=BP=4��x��
��Rt��ABC��
��AB=4��BC=2��
��AC=2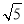 ��
��
��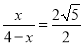 .
.
��� 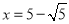 ��
��
����CE��QF��ͬһֱ���ϣ���ͼ3��
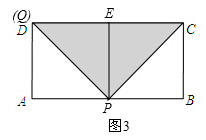
�ߡ�AQP�ա�EQP����CPB�ա�CPE��
��AP=EP=BP��
��2AP=4��
��AP=2��
���㣺�ı����ۺ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2013-2014ѧ�����ʡ�����о��꼶4�µ��п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ���ڵ���Rt��ABC�У���C=90�㣬������DEFG�Ķ���D�ڱ�AC�ϣ���E��F�ڱ�AB�ϣ���G�ڱ�BC�ϣ�

����֤����ADE�ա�BGF��
����������DEFG�����Ϊ16����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�����ʡ���������������꼶�п���Ӧ�Բ�����ѧ�Ծ��������棩 ���ͣ�ѡ����
���۵�������С��һ��ij��ֲ�ﻨ�۵�����ԼΪ0.000037���ˣ���֪1��=1000����,��ô0.000037���˿��ÿ�ѧ��������ʾΪ��������
A��3.7��10��5�� B��3.7��10��6��
C��37��10��7�� D��3.7��10��8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�����ʡʮ���о��꼶4�µ��п�����ѧ�Ծ��������棩 ���ͣ������
�������������ڼ䣬���й��Ӵ��ο�48.16���˴Σ�����������267000000Ԫ��������267000000�ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�����ʡʮ���о��꼶4�µ��п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��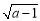 +��b + 2��= 0����ab��ֵΪ�� ��
+��b + 2��= 0����ab��ֵΪ�� ��
A��2 B��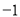 C��1 D��
C��1 D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ���㽭ʡ�����й������п���ģ������ѧ�Ծ��������棩 ���ͣ������
����ֱ�ߺ�Բ�������������������и���һ����Ϊ�����ε����Σ������ε��ĸ����㶼�ھ��εı��ϣ������ͬ��ͼ����Ϊͬһ��.(������ͼ�ۼ�).


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ���㽭ʡ�����й������п���ģ������ѧ�Ծ��������棩 ���ͣ�ѡ����
����˵����
������x�ķ��� �Ľ���x=c��c��0����
�Ľ���x=c��c��0����
��������
 �������Ľ���2�飻
�������Ľ���2�飻
����֪����x��y�ķ����� �����Щ�3��a��1����a=1ʱ��������Ľ�Ҳ�Ƿ���x+y=4��a�Ľ⣻������ȷ���У� ��
�����Щ�3��a��1����a=1ʱ��������Ľ�Ҳ�Ƿ���x+y=4��a�Ľ⣻������ȷ���У� ��
A. �ڢ� B���٢� C.�٢� D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ���㽭����ʮ���н������ž��꼶�ڶ�ѧ��3���¿���ѧ�Ծ��������棩 ���ͣ������
��ͼ���ı���ABCD�ڽ�����O��BD����O��ֱ����AC��BD�ཻ�ڵ�E��AC=BC��DE=2cm��AD=5cm������O�İ뾶Ϊ��____ _ cm.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�����ʡ�п���������ѧ�Ծ��������棩 ���ͣ������
��ͼ����ֱ֪��AB��x�ᡢy��ֱ���A��B��OA=4����OA��OB���ǹ���x�ķ���x2��mx+12=0����ʵ������OBΪֱ������M��AB����C������CM���ӳ���x����N��
��1������M�İ뾶��
��2�����߶�AC�ij���
��3����DΪOA���е㣬��֤��CD����M�����ߣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com