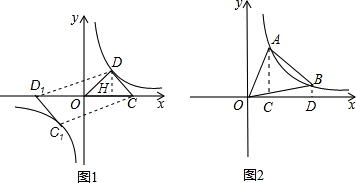
解:(1)过点H作DH⊥CO,
∵点C在x轴的正半轴上且坐标为(4,O),△ODC是以CO为斜边的等腰直角三角形,
∴DH=HO=HC=2,
∴由题可知:D(2,2),
∵点D在反比例函数y=

(k>0)上,
∴k=2×2=4;
(2)连接DD
1,CD
1,
∵线段D
1C
1,由线段DC平移而成,
∴四边形DD
1C
1C为平行四边形,
∴D
1于点C关于原点对称,
∵C(4,0),
∴D
1(-4,0);
(3)∵点A(a,m),B(3a,b)在反比例函数y=

(k>0)的图象上,
∴am=3ab,即b=

,am=4,
分别过点AB作AC⊥x轴,BD⊥x轴,垂足分别为C、D,
∴S
△AOC=S
△BOD=

k=

×4=2,
∴S
△OAB=S
梯形ACDB,即S
△OAB=

(m+b)×(3a-a)=

×

m×2a=
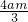
=
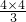
=

.
分析:(1)由于△OCD是等腰直角三角形,不难得出D(2,2),将其代入反比例函数的解析式y=

(k>0)中即可求出k的值;
(2)连接DD
1,CD
1可知四边形DD
1C
1C为平行四边形,根据平行四边形的性质即可得出点D
1的坐标;
(3)先根据动点A(a,m),B(3a,b)在反比例函数y=

(k>0)的图象上,故am=3ab,即b=

,分别过点AB作AC⊥x轴,BD⊥x轴,垂足分别为C、D,由反比例函数系数k的几何意义可知,S
△AOC=S
△BOD=

k=2,故S
△OAB=S
梯形ACDB,由此即可得出结论.
点评:本题考查的是反比例函数综合题,熟知反比例函数系数k的几何意义及反比例函数图象上点的坐标特点是解答此题的关键.

 的图象上,△ODC是以CO为斜边的等腰直角三角形,且C (4,0).
的图象上,△ODC是以CO为斜边的等腰直角三角形,且C (4,0). 上,求点D1的坐标;
上,求点D1的坐标; 的图象上有两个动点A(a,m),B(3a,b),(a>0),求S△OAB的值.
的图象上有两个动点A(a,m),B(3a,b),(a>0),求S△OAB的值.
 解:(1)过点H作DH⊥CO,
解:(1)过点H作DH⊥CO, (k>0)上,
(k>0)上, (k>0)的图象上,
(k>0)的图象上, ,am=4,
,am=4, k=
k= ×4=2,
×4=2, (m+b)×(3a-a)=
(m+b)×(3a-a)= ×
× m×2a=
m×2a=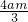 =
=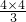 =
= .
. (k>0)中即可求出k的值;
(k>0)中即可求出k的值; (k>0)的图象上,故am=3ab,即b=
(k>0)的图象上,故am=3ab,即b= ,分别过点AB作AC⊥x轴,BD⊥x轴,垂足分别为C、D,由反比例函数系数k的几何意义可知,S△AOC=S△BOD=
,分别过点AB作AC⊥x轴,BD⊥x轴,垂足分别为C、D,由反比例函数系数k的几何意义可知,S△AOC=S△BOD= k=2,故S△OAB=S梯形ACDB,由此即可得出结论.
k=2,故S△OAB=S梯形ACDB,由此即可得出结论.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案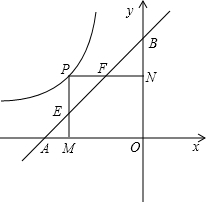 OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;
OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;