
| 2 |
| x |
 OB=2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F��
OB=2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F��| 5 |
| 3 |
| 2 |
| x |
| 2 |
| 2 |
| x |
| 5 |
| 3 |
| 6 |
| 5 |
| 5 |
| 3 |
| 6 |
| 5 |
| 4 |
| 5 |
| 6 |
| 5 |
| 4 |
| 5 |
| 5 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 2 |
| 5 |
| 3 |
| 1 |
| 2 |
| 4 |
| 5 |
| 13 |
| 15 |
| 2 |
| 2 |
| 2 |


 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
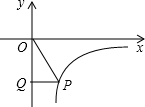 ��ͼ������P�ڷ���������y=-
��ͼ������P�ڷ���������y=-| 2 | 3x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������¦ׯ��2011-2012ѧ����꼶��ѧ�����п�����ѧ���� ���ͣ�022
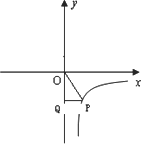
��ͼ������P�ڷ���������![]() ��ͼ���ϣ�����P��PQ��y����Q�����OPQ�����Ϊ________��
��ͼ���ϣ�����P��PQ��y����Q�����OPQ�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2011�괺�����꼶�Ŀ��ۺ�����������ѧ���� ���ͣ�059
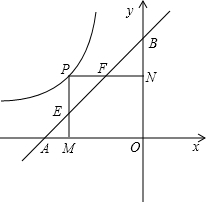
��֪��ͼ������P�ڷ���������y����![]() (x��0)��ͼ�����˶�����A��B�ֱ���X�ᣬY���ϣ���OA��OB��2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F��
(x��0)��ͼ�����˶�����A��B�ֱ���X�ᣬY���ϣ���OA��OB��2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F��

(1)����P��������Ϊ![]() ʱ����OE��OF����E��F��������꼰��EOF�������
ʱ����OE��OF����E��F��������꼰��EOF�������
(2)����P�ں���y����![]() (x��0)��ͼ�����ƶ�������������ΪP(a��b)(��2��a��0��0��b��2��|a|��|b|)�������������䣬̽������AE��EF��BFΪ�ߵ��������������������Σ���֤����Ľ��ۣ�
(x��0)��ͼ�����ƶ�������������ΪP(a��b)(��2��a��0��0��b��2��|a|��|b|)�������������䣬̽������AE��EF��BFΪ�ߵ��������������������Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��x��0����ͼ�����˶�����A��B�ֱ���X�ᣬY���ϣ���OA=
��x��0����ͼ�����˶�����A��B�ֱ���X�ᣬY���ϣ���OA=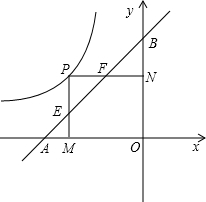 OB=2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F��
OB=2��PM��X����M����AB�ڵ�E��PN��Y���ڵ�N����AB��F�� ʱ����OE��OF����E��F��������꼰��EOF�������
ʱ����OE��OF����E��F��������꼰��EOF������� ��x��0����ͼ�����ƶ�������������ΪP��a��b�� ��-2��a��0��0��b��2��|a|��|b|���������������䣬̽������AE��EF��BFΪ�ߵ��������������������Σ���֤����Ľ��ۣ�
��x��0����ͼ�����ƶ�������������ΪP��a��b�� ��-2��a��0��0��b��2��|a|��|b|���������������䣬̽������AE��EF��BFΪ�ߵ��������������������Σ���֤����Ľ��ۣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com