
已知如图,动点P在反比例函数y=-![]() (x<0)的图象上运动,点A点B分别在X轴,Y轴上,且OA=OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;
(x<0)的图象上运动,点A点B分别在X轴,Y轴上,且OA=OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;

(1)当点P的纵坐标为![]() 时,连OE,OF,求E、F两点的坐标及ΔEOF的面积;
时,连OE,OF,求E、F两点的坐标及ΔEOF的面积;
(2)动点P在函数y=-![]() (x<0)的图象上移动,它的坐标设为P(a,b)(-2<a<0,0<b<2且|a|≠|b|),其他条件不变,探索:以AE、EF、BF为边的三角形是怎样的三角形?并证明你的结论.
(x<0)的图象上移动,它的坐标设为P(a,b)(-2<a<0,0<b<2且|a|≠|b|),其他条件不变,探索:以AE、EF、BF为边的三角形是怎样的三角形?并证明你的结论.
|
(1)解:由条件知A(-2,0),B(0,2)易求得直线AB的解析式为:y=x+2 又∵点P在函数y=- 把x=- 把y= SΔE0F=SΔAOF–SΔAOE= (2)以AE,BF,EF为边的三角形是直角三角形;理由如下: 由条件知ΔAOB是等腰直角三角形,则ΔAME,ΔEPF,ΔFNB均为等腰直角三角形,又-2﹤a﹤0,0﹤b﹤2 AM=2-(-a)=2+a∴AE2=( BN=2-b∴BF2=( PE=PM-EN=PM-AM=b-(2+a)=b-a-2而ab=-2 ∴EF2=( 又|a|≠|b|∴AE≠BF 而(2a2+8a+8)+(2b2-8b+8)=2a2+2b2+8a-8b+16 ∴AE2+BF2=EF2 故以AE,BF,EF为边的三角形是直角三角形; |


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
| 2 |
| x |
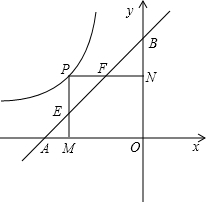 OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;
OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;| 5 |
| 3 |
| 2 |
| x |
查看答案和解析>>
科目:初中数学 来源:江苏省姜堰市娄庄区2011-2012学年八年级下学期期中考试数学试题 题型:022
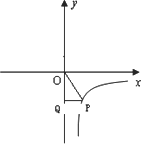
如图,动点P在反比例函数![]() 的图象上,过点P作PQ⊥y轴于Q,则△OPQ的面积为________.
的图象上,过点P作PQ⊥y轴于Q,则△OPQ的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (x<0)的图象上运动,点A点B分别在X轴,Y轴上,且OA=
(x<0)的图象上运动,点A点B分别在X轴,Y轴上,且OA=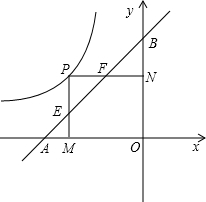 OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F;
OB=2,PM⊥X轴于M,交AB于点E,PN⊥Y轴于点N,交AB于F; 时,连OE,OF,求E、F两点的坐标及△EOF的面积;
时,连OE,OF,求E、F两点的坐标及△EOF的面积; (x<0)的图象上移动,它的坐标设为P(a,b) (-2<a<0,0<b<2且|a|≠|b|),其他条件不变,探索:以AE、EF、BF为边的三角形是怎样的三角形?并证明你的结论.
(x<0)的图象上移动,它的坐标设为P(a,b) (-2<a<0,0<b<2且|a|≠|b|),其他条件不变,探索:以AE、EF、BF为边的三角形是怎样的三角形?并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com