练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点，是正方形的两个顶点，以它的对角线为一边作正方形，以正方形的对角线为一边作正方形，再以正方形的对角线为一边作正方形，…，依次进行下去，则点的坐标是（ ）

    A. B. C. D.

    【答案】A

    【解析】根据已知条件由图中可以得到所在的正方形的对角线长为，所在的正方形的对角线长为，所在的正方形的对角线长为，所在的正方形的对角线长为，所在的正方形的对角线长为，可推出所在的正方形的对角线长为，又因为在x轴负半轴，从而得出答案．

    ∵正方形OBC， ∴O=，所在的象限为第一象限；

    ∴O=，在x轴正半轴；∴O=，所在的象限为第四象限；

    ∴O=，在y轴负半轴；∴O=，所在的象限为第三象限；

    ∴O==8，在x轴负半轴， ∴（－8，0）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=(3-k)x-2k2+18.

    （1）当k为何值时，它的图象经过原点？

    （2）当k为何值时，它的图象经过点（0，-2）？

    （3）当k为何值时，它的图象平行于直线y=-x？

    （4）当k为何值时，y随x增大而减小？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在求1＋3＋32＋33＋34＋35＋36＋37＋38的值时，张红发现：从第二个加数起每一个加数都是前一个加数的3倍，于是她假设：S＝1＋3＋32＋33＋34＋35＋36＋37＋38 ①，然后在①式的两边都乘以3，得：3S＝3＋32＋33＋34＋35＋36＋37＋38＋39 ②，

    ②一①得：3S―S＝39－1，即2S＝39－1，

    ∴S＝.

    得出答案后，爱动脑筋的张红想：如果把“3”换成字母m（m≠0且m≠1），能否求出1＋m＋m2＋m3＋m4＋…＋m2016的值？如能求出，其正确答案是___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是（A，B）的好点．

    （1）如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是（A，B）的好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D______（A，B）的好点，但点D______（B，A）的好点．（请在横线上填是或不是）知识运用：

    （2）如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为-2．数______所表示的点是（M，N）的好点；

    （3）如图3，A、B为数轴上两点，点A所表示的数为-20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以4个单位每秒的速度向左运动，到达点A停止．当经过______秒时，P、A和B中恰有一个点为其余两点的好点？

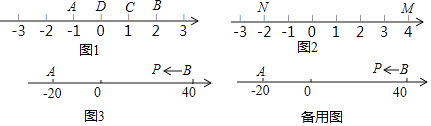
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在我市美化工程招标时，有甲、乙两个工程队投标．经测算：甲队单独完成这项工程需要60天；若由甲队先做20天，剩下的工程由甲、乙合做24天可完成．

    （1）乙队单独完成这项工程需要多少天？

    （2）甲队施工一天，需付工程款3.5万元，乙队施工一天需付工程款2万元．若该工程计划在70天内完成，在不超过计划天数的前提下，是由甲队或乙队单独完成该工程省钱？还是由甲乙两队全程合作完成该工程省钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①是一个长为2m，宽为2n的长方形（m＞n），沿图中虚线用剪刀均匀分民四块小长方形，然后按图②的形状拼成一个正方形．

    （1）图②中阴影部分的正方形的边长是多少？（用代数式表示）

    （2）观察图②写出下列三个代数式：（m+n）2 ， （m﹣n）2 ， mn之间的等量关系．

    （3）若m+n=7，mn=6，求m-n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

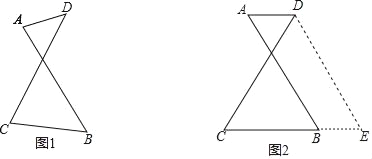
    【题目】如图1有两条长度相等的相交线段AB、CD，它们相交的锐角中有一个角为60°，为了探究AD、CB与CD（或AB）之间的关系，小亮进行了如下尝试：

    （1）在其他条件不变的情况下使得AD∥BC，如图2，将线段AB沿AD方向平移AD的长度，得到线段DE，然后联结BE，进而利用所学知识得到AD、CB与CD（或AB）之间的关系：　 　；（直接写出结果）

    （2）根据小亮的经验，请对图1的情况（AD与CB不平行）进行尝试，写出AD、CB与CD（或AB）之间的关系，并进行证明；

    （3）综合（1）、（2）的证明结果，请写出完整的结论：　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是张亮、李娜两位同学零花钱全学期各项支出的统计图．根据统计图，下列对两位同学购买书籍支出占全学期总支出的百分比作出的判断中，正确的是（ ）

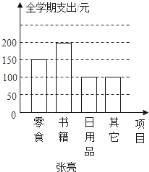
    A. 张亮的百分比比李娜的百分比大 B. 张娜的百分比比张亮的百分比大

    C. 张亮的百分比与李娜的百分比一样大 D. 无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在四边形ABCD中，AE⊥BD于E，CF⊥BD于F，AE＝CF，BF＝DE．求证：四边形ABCD是平行四边形．

    查看答案和解析>>

    同步练习册答案