解:(1)∵直线y=

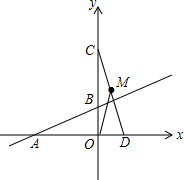
x+1与x轴交于点A,与y轴交于点B,
∴y=0时,x=-3,x=0时,y=1,
∴A点坐标为:(-3,0),B点坐标为:(0,1),
∴OC=3,DO=1,
∴点C的坐标是(0,3),线段AD的长等于4;
(2)∵CM=OM,
∴∠OCM=∠COM.
∵∠OCM+∠ODM=∠COM+∠MOD=90°,
∴∠ODM=∠MOD,
∴OM=MD=CM,
∴点M是CD的中点,
∴点M的坐标为(

,

).
(说明:由CM=OM得到点M在OC在垂直平分线上,所以点M的纵坐标为

,再求出直线CD的解析式,进而求出点M的坐标也可.)
∵抛物线y=x
2+bx+c经过点C,M,
∴
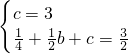
,
解得:
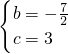
.
∴抛物线y=x
2+bx+c的解析式为:y=x
2-

x+3.
(3)抛物线上存在点P,使得以C,E,F,P为顶点的四边形是菱形.
情形1:如图1,当点F在点C的左边时,四边形CFEP为菱形.
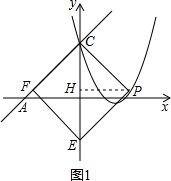
∴∠FCE=PCE,
由题意可知,OA=OC,
∴∠ACO=∠PCE=45°,
∴∠FCP=90°,
∴菱形CFEP为正方形.
过点P作PH⊥CE,垂足为H,
则Rt△CHP为等腰直角三角形.
∴CP=

CH=

PH.
设点P为(x,x
2-

x+3),则OH=x
2-

x+3,PH=x,
∵PH=CH=OC-OH,
∴3-(x
2-

x+3)=x,
解得:x=

∴CP=

CH=

×

=

,
∴菱形CFEP的周长l为:

×4=10

.
情形2:如图2,当点F在点C的右边时,四边形CFPE为菱形.
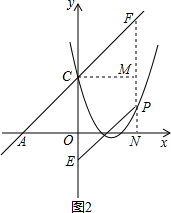
∴CF=PF,CE∥FP.
∵直线AC过点A(-3,0),点C(0,3),
∴直线AC的解析式为:y=x+3.
过点C作CM⊥PF,垂足为M,
则Rt△CMF为等腰直角三角形,CM=FM.
延长PF交x轴于点N,
则PN⊥x轴,∴PF=FN-PN,
设点P为(x,x
2-

x+3),则点F为(x,x+3),
∴FC=

x,FP=(x+3)-(x
2-

x+3)=-x
2+

x,
∴

x=-x
2+

x,
解得:x=

-

,
∴FC=

x=

-2,
∴菱形CFEP的周长l为:(

-2)×4=18

-8.
综上所述,这样的菱形存在,它的周长为10

或18

-8.
分析:(1)首先求出图象与x轴交于点A,与y轴交于点B的坐标,进而得出C点坐标以及线段AD的长;
(2)首先得出点M是CD的中点,即可得出M点坐标,进而利用待定系数法求二次函数解析式;
(3)分别根据当点F在点C的左边时以及当点F在点C的右边时,分析四边形CFPE为菱形得出即可.
点评:此题主要考查了二次函数综合应用以及菱形的判定与性质等知识,根据已知进行分类讨论得出是解题关键.

 如图,已知直线y=
如图,已知直线y= x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD. 解:(1)∵直线y=
解:(1)∵直线y= x+1与x轴交于点A,与y轴交于点B,
x+1与x轴交于点A,与y轴交于点B, ,
, ).
). ,再求出直线CD的解析式,进而求出点M的坐标也可.)
,再求出直线CD的解析式,进而求出点M的坐标也可.)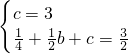 ,
,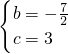 .
. x+3.
x+3.
 CH=
CH= PH.
PH. x+3),则OH=x2-
x+3),则OH=x2- x+3,PH=x,
x+3,PH=x, x+3)=x,
x+3)=x,
 CH=
CH= ×
× =
= ,
, ×4=10
×4=10 .
.
 x+3),则点F为(x,x+3),
x+3),则点F为(x,x+3), x,FP=(x+3)-(x2-
x,FP=(x+3)-(x2- x+3)=-x2+
x+3)=-x2+ x,
x, x=-x2+
x=-x2+ x,
x, -
- ,
, x=
x= -2,
-2, -2)×4=18
-2)×4=18 -8.
-8. 或18
或18 -8.
-8.

 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 如图,已知直线l1:y=
如图,已知直线l1:y=