
【题目】为创建“绿色学校”,绿化校园环境,我校计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵,共花费265元(两次购进同种花草价格相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共30棵,且B种花草的数量不高于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
【答案】(1)A种花草每棵的价格是20元,B种花草每棵的价格是5元.(2)购进A种花草的数量为10棵、B种20棵,费用最省;最省费用是300元.
【解析】
(1)设A种花草每棵的价格x元,B种花草每棵的价格y元,根据第一次分别购进A、B两种花草30棵和15棵,共花费940元;第二次分别购进A、B两种花草12棵和5棵,两次共花费675元;列出方程组,即可解答.
(2)设A种花草的数量为m株,则B种花草的数量为(31-m)株,根据B种花草的数量不少于A种花草的数量的2倍,得出m的范围,设总费用为W元,根据总费用=两种花草的费用之和建立函数关系式,由一次函数的性质就可以求出结论.
解:(1)设A种花草每棵的价格x元,B种花草每棵的价格y元,根据题意得:
![]() ,
,
解得:![]() ,
,
答:A种花草每棵的价格是20元,B种花草每棵的价格是5元.
(2)设A种花草的数量为m株,则B种花草的数量为(30-m)株,
∵B种花草的数量不少于A种花草的数量的2倍,
∴30-m≤2m,
解得:m ≥10,
设购买树苗总费用为W,则
W=20m+5(30-m)
=15m+150
∵k=15>0,W随x的减小而减小.
m是正整数,当m=10时,W最小值=15×10+150=300(元).
答:购进A种花草的数量为10棵、B种20棵,费用最省;最省费用是300元.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】(本题6分)如图,△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上,将△ABC向右平移3格,再向上平移2格.
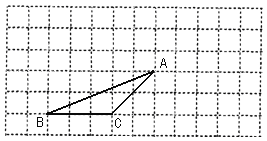
(1)请在图中画出平移后的![]() ;
;
(2)△ABC的面积为 _;
(3)若AB的长约为5.4,求出AB边上的高(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点B按顺时针方向旋转后得到矩形A′BC′D′.若边A′B交线段CD于H,且BH=DH,则DH的值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.
(1)等腰直角三角形是不是“少见的三角形”?
(2)已知如图所示的钝角三角形是一个“少见的三角形”,请你画出分割线的大致位置,并求出顶角的度数;
(3)锐角三角形中有没有“少见的三角形”?如果没有,请说明理由;如果有,请画出图形并求出顶角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ ABC中,AD,AE分别是 △ ABC的高和角平分线,若∠B=30°,∠C=50°.
(1)求∠DAE的度数.
(2)试写出 ∠DAE与∠C-∠B有何关系?(不必证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
A.2:3
B.3:4
C.1:1
D.4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如图: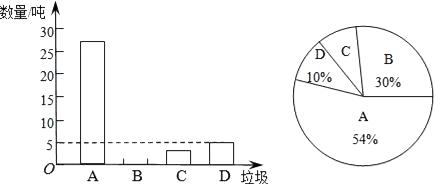
(注:A为可回收物,B为厨余垃圾,C为有害垃圾,D为其他垃圾)
根据图表解答下列问题:
(1)在抽样数据中,产生的有害垃圾共多少吨?
(2)请将条形统计图补充完整;
(3)调查发现,在可回收物中塑料类垃圾占 ![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com