
 ��ͼ����Rt��ABC�У���C=90�㣬AC=BC��AB=6����P�ڱ�AB���˶�������P��PQ��AB������AC-CB�ڵ�Q��Rt��EDF��б��EF������BC�ϣ�DF��AB��DF=AP����DF��AB�ľ���Ϊ$\frac{AP}{2}$�����EDF���ABC�ص�����ͼ�ε����Ϊy���߶�AP�ij�Ϊx��0��x��6��
��ͼ����Rt��ABC�У���C=90�㣬AC=BC��AB=6����P�ڱ�AB���˶�������P��PQ��AB������AC-CB�ڵ�Q��Rt��EDF��б��EF������BC�ϣ�DF��AB��DF=AP����DF��AB�ľ���Ϊ$\frac{AP}{2}$�����EDF���ABC�ص�����ͼ�ε����Ϊy���߶�AP�ij�Ϊx��0��x��6������ ��1��ֻҪ֤����APQ�ǵ���ֱ�������μ��ɽ�����⣮
��2��������DE=DF=AP=PQ����PQ��DE��TC �ı���PQED��ƽ���ı��Σ��ɵ�$\frac{1}{3}$��$\frac{1}{2}$��6��3=x•��6-2x-$\frac{1}{2}$x�����ⷽ�̼��ɣ�
��3���������������ۢ�0��x����2ʱ���ص������ǡ�DEF���ڵ�2��x��3ʱ����ͼ2�У��ص��������ı���DFCG���ֱ���⼴�ɣ�
��4��������������ͼ3�У���PD��BCʱ������ͼ4�У���PD��ABʱ������ͼ5�У���PA=PBʱ����֤PD��AC���ֱ���⼴�ɣ�
��� �⣺��1����CA=CB����C=90�㣬
���A=45�㣬
��PQ��AB��
���APQ=90�㣬
���A=��PQA=45�㣬
��PQ=PA=x��0��x��6����
��2����ͼ1�У�����EQ��PD���ӳ�ED��AB��G����FH��AB��H�����ı���DGFH�Ǿ��Σ�DF=GH=x��FH=BH=$\frac{1}{2}$x��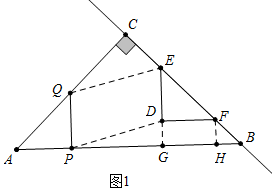
������DE=DF=AP=PQ����PQ��DE��
���ı���PQED��ƽ���ı��Σ�
��$\frac{1}{3}$��$\frac{1}{2}$��6��3=x•��6-2x-$\frac{1}{2}$x����
���x=$\frac{6��\sqrt{6}}{5}$��
��x=$\frac{6��\sqrt{6}}{5}$ʱ����Q��P��D��EΪ������ı��ε�����ǡ�ABC�������$\frac{1}{3}$��
��3���ٵ�DE+DG=3ʱ����x+$\frac{1}{2}$x=3��x=2ʱ����E���C�غϣ�
��0��x����2ʱ���ص������ǡ�DEF��y=$\frac{1}{2}$x2
�ڵ�2��x��3ʱ����ͼ2�У��ص��������ı���DFCG��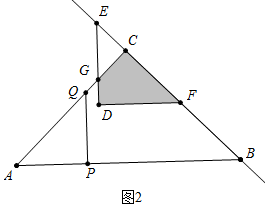
y=S��DEF-S��ECG=$\frac{1}{2}$x2-��x+$\frac{1}{2}$x-3��2=-$\frac{7}{4}$x2+9x-9��
����������y=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2}}&{��0��x��2��}\\{-\frac{7}{4}{x}^{2}+9x-9}&{��2��x��3��}\end{array}\right.$��
��4������ͼ3�У���PD��BCʱ���ӳ�PD��BC��G�����PGB�ǵ���ֱ�������Σ�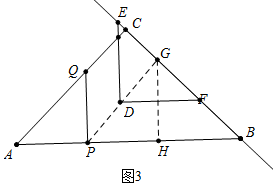
��GH��PB��H��
��GH=$\frac{1}{2}$PB��
��x=$\frac{1}{2}$��6-x����
��x=2��
��PA=DF=2��PB=4��PG=2$\sqrt{2}$��DG=$\sqrt{2}$��
��PD=$\sqrt{2}$��
����ͼ4�У���PD��ABʱ��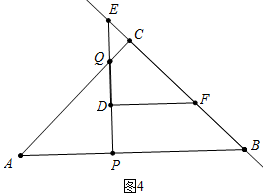
������x+x+$\frac{1}{2}$x=6��
x=$\frac{12}{5}$��
��PA=DF=DE=$\frac{12}{5}$��PB=PE=$\frac{18}{5}$��
��PD=PE-DE=$\frac{6}{5}$��
����ͼ5�У���PA=PBʱ����֪DF�ǡ�ABC����λ�ߣ�AD=CD����PA=PC����PD��AC����ʱx=3��PD=$\frac{3\sqrt{2}}{2}$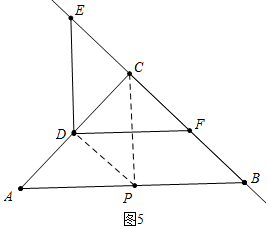
����������PD=$\sqrt{2}$��$\frac{6}{5}$��$\frac{3\sqrt{2}}{2}$ʱ��ֱ��PD���ABC�ıߴ�ֱ��
���� ���⿼���������ۺ��⡢����ֱ�������ε����ʡ�ƽ���ı��ε��ж������ʡ��������������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����̣��÷��̵�˼��˼�����⣬�����п�ѹ���⣮


 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{a}^{6}}{{a}^{3}}$=a2 | B�� | $\frac{2a{b}^{2}}{6{a}^{2}{b}^{2}}$=$\frac{1}{3}$ | C�� | $\frac{m+n}{{m}^{2}+mn}$=$\frac{1}{m}$ | D�� | $\frac{x-y}{x-y}$=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
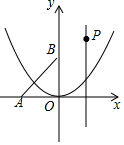 ����ֱ�ǡ�ABO��ֱ������ϵ��λ����ͼ��ʾ��OΪԭ�㣬��BΪy��������������һ�㣬��A��x�Ḻ�����ϣ�PΪֱ��x=1����һ�㣬����ABO�Ƶ�P˳ʱ����ת90�㣬�õ���A��B��O�䣮
����ֱ�ǡ�ABO��ֱ������ϵ��λ����ͼ��ʾ��OΪԭ�㣬��BΪy��������������һ�㣬��A��x�Ḻ�����ϣ�PΪֱ��x=1����һ�㣬����ABO�Ƶ�P˳ʱ����ת90�㣬�õ���A��B��O�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
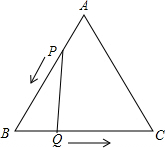 ��֪����ͼ����ABC�DZ߳�Ϊ4cm�ĵȱ������Σ�����P��Qͬʱ��A��B����������ֱ���AB��BC���������ƶ������ǵ��ٶȶ���1cm/s������P�����Bʱ��P��Q����ֹͣ�˶������P���˶�ʱ��t��s����������и����⣺
��֪����ͼ����ABC�DZ߳�Ϊ4cm�ĵȱ������Σ�����P��Qͬʱ��A��B����������ֱ���AB��BC���������ƶ������ǵ��ٶȶ���1cm/s������P�����Bʱ��P��Q����ֹͣ�˶������P���˶�ʱ��t��s����������и����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
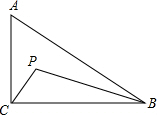 ��ͼ��Rt��ABC�У�AC��BC��AC=8��BC=12��P�ǡ�ABC�ڲ���һ�����㣬�������PCA=��PBC�����߶�AP������СֵΪ4��
��ͼ��Rt��ABC�У�AC��BC��AC=8��BC=12��P�ǡ�ABC�ڲ���һ�����㣬�������PCA=��PBC�����߶�AP������СֵΪ4���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com