
分析 (1)求出销售量,根据政府每件补贴2元,即可解决问题.
(2)构建二次函数,利用二次函数的性质解决问题即可.
(3)根据条件确定出自变量的取值范围,求出y的最小值即可解决问题.
解答 解:(1)当x=18时,y=-10x+400=-10×18+400=220,
220×(12-10)=220×2=440元.
即政府这个月为他承担的总差价为440元.
(2)依题意得,w=(x-10)(-10x+400)
=-10x2+500x-4000
=-10(x-25)2+2250
∵a=-10<0,
∴当x=25时,w有最大值2250元.
即当销售单价定为25元时,每月可获得最大利润2250元.
(3)由题意得:-10x2+500x-4000=2000,
解得:x1=20,x2=30.
∵a=-10<0,抛物线开口向下,
当20≤x≤30时,2250≥w≥2000.
又∵x≤24,
∴当20≤x≤24时,w≥2000.
∴当x=24时,政府每个月为他承担的总差价最小,y=-24×10+400=160,
160×2=320,
∴政府每个月为他承担的总差价最小值320元.
即销售单价定为24元时,政府每个月为他承担的总差价最少为320元.
点评 本题考查二次函数的应用、一次函数的应用、利润、销售量、单价之间的关系等知识,解题的关键是理解题意,学会构建二次函数解决最值问题,学会利用一次函数的增减性,解决实际问题中的最值问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P在边AB上运动,过点P作PQ⊥AB交折线AC-CB于点Q,Rt△EDF的斜边EF在射线BC上,DF∥AB,DF=AP,且DF与AB的距离为$\frac{AP}{2}$,设△EDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6)
如图,在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P在边AB上运动,过点P作PQ⊥AB交折线AC-CB于点Q,Rt△EDF的斜边EF在射线BC上,DF∥AB,DF=AP,且DF与AB的距离为$\frac{AP}{2}$,设△EDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
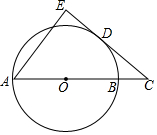 如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA
如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com