
在平面直角坐标系中,我们不妨把横坐标和纵坐标相等的点叫“梦之点”,例如点(1,1),(-2,-2),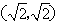 ,…都是“梦之点”,显然“梦之点”有无数个。
,…都是“梦之点”,显然“梦之点”有无数个。
(1)若点P(2,m)是反比例函数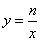 (n为常数,n≠0)的图像上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图像上的“梦之点”,求这个反比例函数的解析式;
(2)函数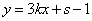 (k,s为常数)的图像上存在“梦之点”吗?若存在,请求出“梦之点”的坐标,若不存在,说明理由;
(k,s为常数)的图像上存在“梦之点”吗?若存在,请求出“梦之点”的坐标,若不存在,说明理由;
(3)若二次函数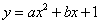 (a,b是常数,a>0)的图像上存在两个“梦之点”A
(a,b是常数,a>0)的图像上存在两个“梦之点”A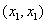 ,
,
B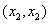 ,且满足-2<
,且满足-2<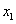 <2,
<2,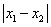 =2,令
=2,令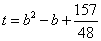 ,试求t的取值范围。
,试求t的取值范围。
科目:初中数学 来源: 题型:
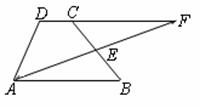
如图,已知AB//DC,E是BC的中点,AE,DC的延长线交于点F;
(1)求证:△ABE≌△FCE;
(2)连接AC,BF.则四边形ABFC是什么特殊的四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
2014年南京青奥会某项目6名礼仪小姐的身高如下(单位:cm):168,166,168,167,169,168,则她们身高的众数是 cm,极差是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【问题提出】
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
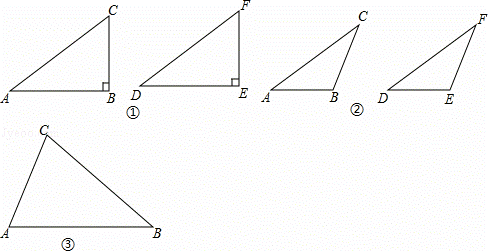
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 HL ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 ∠B≥∠A ,则△ABC≌△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
.在表达式S=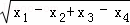 中,x1、x2、x3、x4是1、2、3、4的一种排列(即:x1、x2、x3、x4取1、2、3、4中的某一个数,且x1、x2、x3、x4互不相同).则使S为实数的不同排列的种数有 _________ 种.
中,x1、x2、x3、x4是1、2、3、4的一种排列(即:x1、x2、x3、x4取1、2、3、4中的某一个数,且x1、x2、x3、x4互不相同).则使S为实数的不同排列的种数有 _________ 种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com