
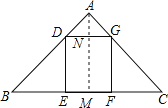
【题目】如图1,在△ABC中,AB=AC=5,BC=6,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上.
(1)求正方形DEFG的边长;
(2)如图2,在BC边上放两个小正方形DEFG、FGMN,则DE= .

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)过点作AM⊥BC于点M,由AB=AC=10,BC=16,根据等腰三角形的性质与勾股定理,即可求得AM的长,又由四边形DEFG是矩形,易证得△ADG∽△ABC,设MN=DE=x,由相似三角形对应高的比等于相似比,即可得方程![]() ,则可表示出DG的长,由正方形的性质可得DE=DG,可得结果;
,则可表示出DG的长,由正方形的性质可得DE=DG,可得结果;
(2)由题意得:DN=2DE,由(1)知:![]() ,即可得到结论.
,即可得到结论.
解:过点作AM⊥BC于点M,
∵AB=AC=5,BC=6,
∴BM=![]() BC=3,
BC=3,
在Rt△ABM中,AM=![]() =4,
=4,
∵四边形DEFG是矩形,
∴DG∥EF,DE⊥BC,
∴AN⊥DG,四边形EDMN是矩形,
∴MN=DE,
设MN=DE=x,
∵DG∥EF,
∴△ADG∽△ABC,
∴DG:BC=AN:AM,
∴![]() ,
,
解得:DG=﹣![]() x+6,
x+6,
∵四边形DEFG为正方形,
∴DE=DG,即x=﹣![]() x+6,
x+6,
解得x=![]() ,
,
∴正方形DEFG的边长为![]() ;
;
(2)由题意得:DN=2DE,
由(1)知:![]() ,
,
∴DE=![]() .
.
故答案为:![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
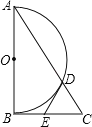
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,OE垂直于弦AB,垂足为点D,交⊙O于点C,∠EAC=∠CAB.
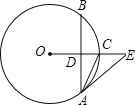
(1)求证:直线AE是⊙O的切线;
(2)若AB=8,sin∠E=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中是确定事件的为( )
A. 两条线段可以组成一个三角形 B. 打开电视机正在播放动画片
C. 车辆随机经过一个路口,遇到绿灯 D. 掷一枚均匀的骰子,掷出的点数是奇数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三个内角互不相等的△ABC中,最小的内角为∠A,则在下列四个度数中,∠A最大可取( )
A. 30° B. 59° C. 60° D. 89°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方形在平面直角坐标系中三个顶点的坐标为(-2,-3),(-2,1),(2,1),则第四个顶点的坐标为( )
A. (2,2) B. (3,2) C. (2,-3) D. (2,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com