
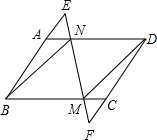
 如图,在平行四边形ABCD中,延长BA到点E,延长DC到点F,使AE=CF,连接EF,分别交AD、BC于点N、M,连接BN、DM.
如图,在平行四边形ABCD中,延长BA到点E,延长DC到点F,使AE=CF,连接EF,分别交AD、BC于点N、M,连接BN、DM.
|


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
| 3 |
| 4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
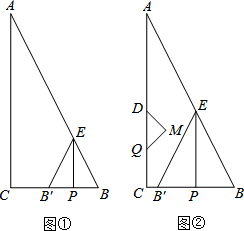 如图①,在直角△ABC中,∠C=90°,AC=8cm,BC=4cm.动点P在线段BC上以1cm/s的速度从点B运动到点C.过点P作PE⊥BC与AB交于点E,以PE为对称轴将PE右侧的图形翻折得到△B′PE,设点P的运动时间为x(s).
如图①,在直角△ABC中,∠C=90°,AC=8cm,BC=4cm.动点P在线段BC上以1cm/s的速度从点B运动到点C.过点P作PE⊥BC与AB交于点E,以PE为对称轴将PE右侧的图形翻折得到△B′PE,设点P的运动时间为x(s).查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.2元;乙种使用者不缴月租费,每通话1分钟,付话费0.6元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.
某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.2元;乙种使用者不缴月租费,每通话1分钟,付话费0.6元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
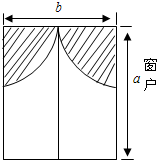 小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成(半径相同,π取3)
小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成(半径相同,π取3)| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com