
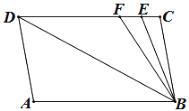
【题目】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由.
(2)求∠DBE的度数.
(3)若把AD左右平行移动,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出此时∠ADB的度数;若不存在,请说明理由.
【答案】(1) AD∥BC,理由见解析;(2) 40°;(3)存在,∠ADB=60°
【解析】试题分析:(1)根据平行线的性质,以及等量代换证明∠ADC+∠C=180°,即可证得AD∥BC;(2)由直线AB∥CD,根据两直线平行,同旁内角互补,即可求得∠ABC的度数,又由∠DBE=![]() ∠ABC,即可求得∠DBE的度数.
∠ABC,即可求得∠DBE的度数.
(3)首先设∠ABD=∠DBF=∠BDC=x°,由直线AB∥CD,根据两直线平行,同旁内角互补与两直线平行,内错角相等,可求得∠BEC与∠ADB的度数,又由∠BEC=∠ADB,即可得方程:x°+40°=80°-x°,解此方程即可求得答案.
试题解析:(1)AD∥BC
理由:∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)∵AB∥CD,
∴∠ABC=180°-∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE=![]() ∠ABF+
∠ABF+![]() ∠CBF=
∠CBF=![]() ∠ABC=40°;
∠ABC=40°;
(3)存在.
理由:设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°-∠A=80°,
∴∠ADB=80°-x°.
若∠BEC=∠ADB,
则x°+40°=80°-x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
, ![]() 分别是
分别是![]() 轴正半轴,
轴正半轴, ![]() 轴正半轴上两动点,
轴正半轴上两动点, ![]() ,
, ![]() ,以
,以![]() ,
, ![]() 为邻边构造矩形
为邻边构造矩形![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
, ![]() 为顶点,
为顶点, ![]() 轴于点
轴于点![]() .
.
(![]() )求
)求![]() ,
, ![]() 的长(结果均用含
的长(结果均用含![]() 的代数式表示);
的代数式表示);
(![]() )当
)当![]() 时,求该抛物线的表达式;
时,求该抛物线的表达式;
(![]() )在点
)在点![]() 在整个运动过程中,若存在
在整个运动过程中,若存在![]() 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的![]() 的值.
的值.
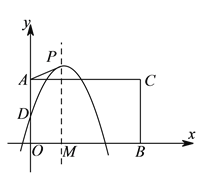
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=![]() (x+1)2-1的图象.
(x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月初,在抵御新冠肺炎的工作中,全国各地口罩严重供应不足,某乡镇企业缝纫车间立即转岗做口罩以供应本地志愿者和卫生系统,该车间有技术工人15人,生产部为了合理制定口罩的日生产定额,统计了15人某天加工口罩数如下:
车间15名工人某一天加工口罩个数统计表
加工零件数/个 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)求这一天15名工人加工口罩数的平均数、中位数和众数.
(2)为了提高大多数工人的积极性,管理者准备试行“每天定额生产,超产有奖”的措施,假如你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目:初中数学 来源: 题型:
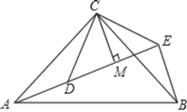
【题目】如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.
(1)求∠AEB的度数;
(2)线段CM、AE、BE之间存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 如图1,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF,四边形AEGF是矩形,写出矩形AEGF的面积y与BE的长x之间的函数关系式;
(2) 如图2,已知一长方形打印纸长20 cm,宽15 cm,现在要在打印纸上打印文稿,上下左右各留出一定距离.设留出的距离均为x cm,打印文稿面积为y cm2,试写出y与x之间的关系式,并求出x的取值范围.
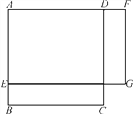
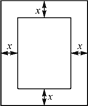
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为m,n,p,并且设置了相应的垃圾箱,“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1 000吨生活垃圾,数据统计如下(单位:吨):
A | B | C | |
m | 400 | 100 | 100 |
n | 30 | 240 | 30 |
p | 20 | 20 | 60 |
请根据以上信息,试估计“厨房垃圾”投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD,尺规作图:以点A为圆心,AB的长为半径画弧交AD于点F,分别以点B,F为圆心,以大于 BF的长为半径画弧交于点G,做射线AG交BC与点E,若BF=12,AB=10,则AE的长为( ).

A.17B.16C.15D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,D、E是BC边上的点,连接AD、AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)求证:△ABD≌△ACD′;
(2)如图2,若∠BAC=120°,探索BD,DE,CE之间满足怎样的数量关系时,△CD′E是正三角形;
(3)如图3,若∠BAC=90°,求证:DE2=BD2+EC2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com