
【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM. 
(1)求证:EF= ![]() AC.
AC.
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
【答案】
(1)证明:∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∵点F为AC的中点,
∴EF= ![]() AC
AC
(2)解:∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM
【解析】(1)根据等腰三角形三线合一的性质可得CE⊥BD,再根据直角三角形斜边上的中线等于斜边的一半可得EF= ![]() AC;(2)判断出△AEC是等腰直角三角形,根据等腰直角三角形的性质可得EF垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AM=CM,然后求出CD=AM+DM,再等量代换即可得解.
AC;(2)判断出△AEC是等腰直角三角形,根据等腰直角三角形的性质可得EF垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AM=CM,然后求出CD=AM+DM,再等量代换即可得解.
【考点精析】关于本题考查的等腰直角三角形和直角三角形斜边上的中线,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形斜边上的中线等于斜边的一半才能得出正确答案.


科目:初中数学 来源: 题型:
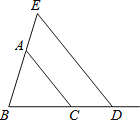
【题目】如图,已知△ABC.
(1)若AB=4,AC=5,则BC边的取值范围是 ;
(2)点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在图①中以P为顶点画∠P,使∠P的两边分别和∠1的两边垂直;
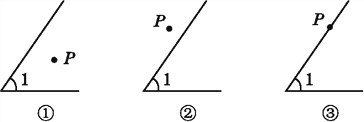
(2)量一量∠P和∠1的度数,它们之间的数量关系是 ;
(3)同样在图②和图③中以P为顶点作∠APB,使∠APB的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB和∠1之间的数量关系(不要求写出理由).
图②: ,
图③: ;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为18 cm的圆,从中心挖去一个正方形,当挖去的正方形的边长由小变大时,剩下部分的面积也随之发生变化.

(1)若挖去的正方形边长为x(cm),剩下部分的面积为y(cm2),则y与x之间的关系式是什么?
(2)当挖去的正方形的边长由1 cm变化到9 cm时,剩下部分的面积由____变化到____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com