
解:(1)当∠A=30°时,CD是⊙O的切线.
理由:连接OC,如图.
方法一:∵OA=OC,∴∠A=∠C=30°
∴∠COD=∠A+∠OCA=60°
又∵AC=CD,∴∠D=∠A=30°
∴∠OCD=180°-∠COD-∠D=90°
所以CD是⊙O的切线
方法二:∵CD是⊙O的切线
∴∠OCD=90°
∵AC=CD,∴∠D=∠A=30°
又∵OA=OC,∴∠COD=2∠A=2∠D
∴∠A=30°
(2)∵OB=OC,∠COD=60°,
∴△BOC是等边三角形,∴∠OCB=60°
∴∠BCD=∠OCD-∠OCB=90°-60°
∴∠BCD=∠D
∴OC=BC=BD=

.
CD=OC•tan60°=

×

=3.
∴S
阴影=S
△OCD-S
扇形BOC=

×

×3-
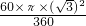
=

-

.
分析:(1)连接OC,可用不同的方法证明,根据OA=OC,则∠A=∠C=30°,可求出∠OCD=90°,即CD是⊙O的切线;
(2)可证明△BOC是等边三角形,则∠OCB=60°,可得出∠BCD=∠D,由三角函数CD=OC•tan60°,得出CD的长,因为S
阴影=S
△OCD-S
扇形BOC,所以可得出答案.
点评:本题考查了切线的判定和性质、扇形面积的计算以及解直角三角形的内容,比较简单要熟练掌握.

 D=
D= .
. 解:(1)当∠A=30°时,CD是⊙O的切线.
解:(1)当∠A=30°时,CD是⊙O的切线. .
. ×
× =3.
=3. ×
× ×3-
×3-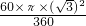 =
= -
- .
.

 (2012•黔东南州)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
(2012•黔东南州)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.