Question

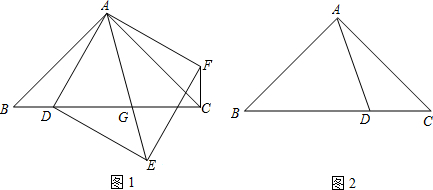
已知，△ABC是等腰直角三角形，∠BAC=90°，BC=2，D是线段BC上一点，以AD为边，在AD的右侧作正方形ADEF．直线AE与直线BC交于点G，连接CF．

（1）如图1，当BD＜1时，求证：△ACF≌△ABD；

（2）如图2，当BD＞1时，请在图中作出相应的图形，猜测线段CF与线段BD的关系，并说明理由；

（3）连接GF，判断当线段BD为何值时，△GFC是等腰三角形．

Answer 1

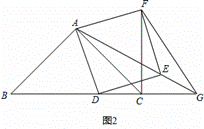（2）作图如右：…………………………………（4分）

猜测：CF=BD，CF⊥BD………………………（6分）

理由是：同（1）可得△ABD≌△ACF

∴CF=BD，∠ACF=∠ABD=∠ACB=45°

∴∠FCB=90°，∴CF⊥BD………………………（8分）

（3）连接GF

∵AE是正方形ADEF的对角线

∴∠FAE=∠DAE=45°

又AD=AF，AG=AG

∴△AFG≌△ADG

∴FG=DG………………………………………………（10分）

若Rt△CFG是等腰三角形，则CG=CF

设CF=x，得CG=CF=BD=x

①如图3，当BD＜1时，FG=DG=2﹣2x

在Rt△CFG中，根据勾股定理得

FG²=CG²+CF²

∴（2﹣2x）²=2x²

解得：x₁=2+＞1（舍去），x₂=2﹣…………（12分）

②如图4，当BD＞1时，∵CG=BD

∴FG=DG=BC=2

在Rt△CFG中，根据勾股定理得

FG²=CG²+CF²，2²=2x²

解得：x₁=﹣（舍去），x₂=

综上所得，当BD等于2﹣ 或 时，

△CFG是等腰三角形…