若多项式x2+kx﹣2x+3中不含有x的一次项，则k=__________．
科目：初中数学 来源： 题型：
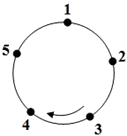
如图，圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五个点按顺时针方向依次编号为1，2，3，4，5，若从某一点开始，沿圆周顺时针方向行走，点的编号是数字几，就走几段弧长，则称这种走法为一次“移位”．如：小明在编号为3的点，那么他应走3段弧长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的点，然后从1→2为第二次“移位”．
（1）①若小明从编号为3的点开始，第三次“移位”后，他到达编号为__________的点；
②若小明从编号为2的点开始，第一次“移位”后，他到达编号为___________的点，若小明从编号为2的点开始，第四次“移位”后，他到达编号为__________的点，第2015次“移位”后，他到达编号为__________的点．
（2）若将圆进行二十等份，按照顺时针方向依次编号为1，2，3，…，20，小明从编号为2的点开始，沿顺时针方向行走，经过2012次“移位”后，他到达编号为__________的点．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
：2．
的点位置最近的数是( )
的值为正整数，你所取的x的值是__________．
的系数是__________，次数是__________．
﹣1
﹣
）÷（﹣
）；
等于（ ）
C．2 D．