
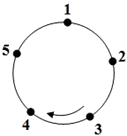
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.
(1)①若小明从编号为3的点开始,第三次“移位”后,他到达编号为__________的点;
②若小明从编号为2的点开始,第一次“移位”后,他到达编号为___________的点,若小明从编号为2的点开始,第四次“移位”后,他到达编号为__________的点,第2015次“移位”后,他到达编号为__________的点.
(2)若将圆进行二十等份,按照顺时针方向依次编号为1,2,3,…,20,小明从编号为2的点开始,沿顺时针方向行走,经过2012次“移位”后,他到达编号为__________的点.
【考点】规律型:图形的变化类.
【分析】(1)①根据移位的定义,进行计算即可得解;
②根据移位的定义,结合图形第一次“移位”走4段弧长,然后依次进行计算即可得到第四次“移位”的位置,再根据规律求出第2015次“移位”的位置;
(2)根据移位的定义,找出前几次的移位到达的数字编号,找出规律,然后根据规律即可求出第2012次的移位到达的数字编号.
【解答】解:(1)①从编号为3的点开始,第一次“移位”到达1,
第二次“移位”到达2,
第三次“移位”到达4;
②从编号为2的点开始,第一次“移位”到达4,
第二次“移位”到达3,
第三次“移位”到达1,
第四次“移位”到达2;
第五次“移位”到达4,
…
依此类推,每4次为一组“移位”循环,
∴2015÷4=503…3,
∴第2015次“移位”后与第3次移位到达的数字编号相同,为1;
(2)从编号为2的点开始,第一次“移位”到达4,
第二次“移位”到达8,
第三次“移位”到达16,
第四次“移位”到达12,
第五次“移位”到达4,
第六次“移位”到达8;
第七次“移位”到达16,
第八次“移位”到达12,
第九次“移位”到达4,
第10次“移位”到达8,
…
依此类推,从第二次开始,每4次移位为一组“移位”循环,
∴÷4=502…3,
∴2012次“移位”后,他到达编号为第503次循环的第三次“移位”,与第四次的移位到达的编号相同,到达12.
故答案为:(1)①4 ②4;2;1;(2)12.
【点评】本题是对图形变化规律的考查,读懂题目信息,根据“移位”的定义,找出其变化循环的规律是解题的关键.


科目:初中数学 来源: 题型:
对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.
(1)计算2⊙(﹣3)的值;
(2)①当a,b在数轴上的位置如图所示时,化简a⊙b;
②当a⊙b=a⊙c时,是否一定有b=c或者b=﹣c?若是,则说明理由;若不是,则举例说明.
(3)已知(a⊙a)⊙a=8+a,求a的值.
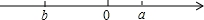
查看答案和解析>>
科目:初中数学 来源: 题型:
某天上午,出租车司机小王在东西向的公路上营运,规定向东为正,向西为负。出租车行程如下:(单位:千米)+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6
(1)小王将最后一名乘客送到目的地时,他离出发点多远?
(2)若汽车耗油量为a升/千米,这天上午小王共耗油多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com