
对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.
(1)计算2⊙(﹣3)的值;
(2)①当a,b在数轴上的位置如图所示时,化简a⊙b;
②当a⊙b=a⊙c时,是否一定有b=c或者b=﹣c?若是,则说明理由;若不是,则举例说明.
(3)已知(a⊙a)⊙a=8+a,求a的值.
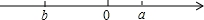
【考点】有理数的混合运算;数轴.
【专题】计算题;新定义.
【分析】(1)原式利用题中的新定义计算即可得到结果;
(2)①根据数轴上点的位置判断出a+b与a﹣b的正负,利用绝对值的代数意义计算即可得到结果;
②当a⊙b=a⊙c时,不一定有b=c或者b=﹣c,举例即可;
(3)分类讨论a的正负,利用新定义将已知等式化简,即可求出a的值.
【解答】解:(1)根据题中的新定义得:2⊙(﹣3)=|2+(﹣3)|+|2﹣(﹣3)|=1+5=6;
(2)①从a,b在数轴上的位置可得a+b<0,a﹣b>0,
∴a⊙b=|a+b|+|a﹣b|=﹣(a+b)+(a﹣b)=﹣2b;
②由a⊙b=a⊙c得:|a+b|+|a﹣b|=|a+c|+|a﹣c|,
不一定有b=c或者b=﹣c,
例如:取a=5,b=4,c=3,则|a+b|+|a﹣b|=|a+ c|+|a﹣c|=10,
c|+|a﹣c|=10,
此时等式成立,但b≠c且b≠﹣c;
(3)当a≥0时,(a⊙a)⊙a=2a⊙a=4a=8+a,
解得:a=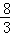 ;
;
当a<0时,(a⊙a)⊙a=(﹣2a)⊙a=﹣4a=8+a,
解得:a=﹣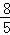 .
.
【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
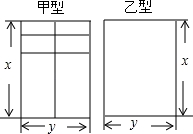
如图所示,是两种长方形塑钢窗框,已知窗框的长都是x米,窗框的宽都是y米,若一用户装修房屋,需要甲型窗框5个,乙型窗框3个,求共需要塑钢多少米(用含x、y的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
(直接写出每小问的结果)经检测,某棵小树在1~10年间的生长高度 符合一定的规律(如表):
符合一定的规律(如表):
| 年份 | 树高(cm) |
| 1 | 200 |
| 2 | 220 |
| 3 | 240 |
| 4 | 260 |
| 5 | 280 |
| … | … |
| 10 |
(1)第10年,这棵小树的高度为__________cm.
(2)树高h(cm)与年份n(1≤n≤10)之间的数量关系是h=__________(用含n的代数式表示h).
(3)如果把树高300cm称为标准树高,记为0cm,超过标准的高度记为正数,不足标准的高度记为负数,那么第2年的树高应记为__________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
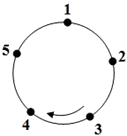
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.
(1)①若小明从编号为3的点开始,第三次“移位”后,他到达编号为__________的点;
②若小明从编号为2的点开始,第一次“移位”后,他到达编号为___________的点,若小明从编号为2的点开始,第四次“移位”后,他到达编号为__________的点,第2015次“移位”后,他到达编号为__________的点.
(2)若将圆进行二十等份,按照顺时针方向依次编号为1,2,3,…,20,小明从编号为2的点开始,沿顺时针方向行走,经过2012次“移位”后,他到达编号为__________的点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com