解:(1)把点M(-

,2)代入y=kx+3,
得-

k+3=2,即k=

,
则直线AM是y=

x+3,
由

x+3=0,得x=-3

,
即点A(-3

,0),
过点M作MN⊥x轴于N,
在Rt△MAN中,则AN=2

,MN=2,
则tan∠MAN=

,
则∠MAO=∠MAN=30°;
(2)设平移后的抛物线顶点为P(h,0),其中h>0,

则解析式变为y=

(x-h)
2,
令x=0,得y=

h
2,
所以,点E(0,

h
2),
∵点F在平移后的抛物线上,且EF∥x轴,
∴点F(2h,

h
2),
∵点F还在直线y=

x+3上,
∴

h
2=

h+3,
整理得,h
2-2

h-9=0,
解得,h
1=3

,h
2=-

(舍去),
故所求抛物线的顶点坐标是(3

,0).
分析:(1)把点M的坐标代入直线y=kx+3计算求出k值,从而得到直线解析式,然后求出与x轴的交点坐标,过M作MN⊥x轴于点N,求出AN、MN的长度,再根据∠MAN的正切值求解即可;
(2)设平移后的抛物线顶点为P(h,0),令x=0求出点E的坐标,再根据EF∥x轴得到点F的纵坐标,然后代入抛物线解析式计算求出h的值,即可得解.
点评:本题是二次函数综合题型,主要考查了待定系数法求一次函数解析式,特殊角的三角函数,二次函数图象的几何变化,(2)利用顶点式形式表示出二次函数解析式是解题的关键.

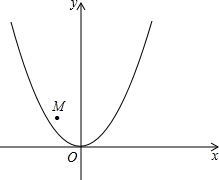 如图,已知点M(-
如图,已知点M(- ,2)和抛物线y=
,2)和抛物线y=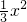 ,O为直角坐标系的原点.
,O为直角坐标系的原点. ,2)代入y=kx+3,
,2)代入y=kx+3, k+3=2,即k=
k+3=2,即k= ,
, x+3,
x+3, x+3=0,得x=-3
x+3=0,得x=-3 ,
, ,0),
,0), ,MN=2,
,MN=2, ,
,
 (x-h)2,
(x-h)2, h2,
h2, h2),
h2), h2),
h2), x+3上,
x+3上, h2=
h2= h+3,
h+3, h-9=0,
h-9=0, ,h2=-
,h2=- (舍去),
(舍去), ,0).
,0).

 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设