
 ,x与y的对应值如下表:
,x与y的对应值如下表:
 1 2 ﹣2 ﹣1 ﹣
1 2 ﹣2 ﹣1 ﹣ 的解为 ;不等式﹣x+1>﹣
的解为 ;不等式﹣x+1>﹣ 的解集为 .
的解集为 . 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源:不详 题型:解答题
 (x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.
(x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 x﹣1与反比例函数
x﹣1与反比例函数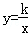 (x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )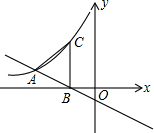
| A.﹣2 | B.﹣4 | C.﹣6 | D.﹣8 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+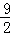 与双曲线y=
与双曲线y= (m>0)的交点.
(m>0)的交点.
 (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN= AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
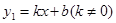 与反比例函数
与反比例函数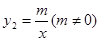 ,在同一直角坐标系中的图象如图所示,若
,在同一直角坐标系中的图象如图所示,若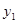 ﹥
﹥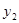 ,则x的取值范围是( )
,则x的取值范围是( )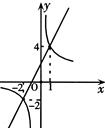
A.-2﹤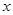 ﹤0或 ﹤0或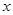 ﹥1? ﹥1? | B.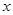 ﹤-2或0﹤ ﹤-2或0﹤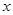 ﹤1 ﹤1 |
C.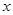 ﹥1 ﹥1 | D.-2﹤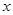 ﹤1 ﹤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com