
 )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+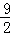 与双曲线y=
与双曲线y= (m>0)的交点.
(m>0)的交点.
 (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN= AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.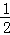 且m=4 (2)不存在,理由见解析
且m=4 (2)不存在,理由见解析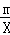 ,可用含m的代数式表示它的纵坐标;同理可表示点B坐标,再代入方程组
,可用含m的代数式表示它的纵坐标;同理可表示点B坐标,再代入方程组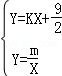 即可求m和k的值;
即可求m和k的值;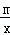 (m>0)上,AC∥y轴,BC∥x轴,
(m>0)上,AC∥y轴,BC∥x轴,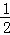 ).(1分)
).(1分)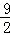 上,
上,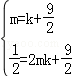 (2分)
(2分)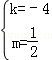 或
或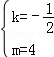 (4分)
(4分)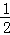 时,点A,B的坐标都是(1,
时,点A,B的坐标都是(1,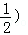 ,不合题意,应舍去;
,不合题意,应舍去;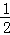 且m=4时,点A,B的坐标分别为(1,4),(8,
且m=4时,点A,B的坐标分别为(1,4),(8,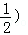 ,符合题意.
,符合题意.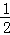
 AB.
AB.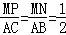 ,(7分)
,(7分) )(1<x<8),
)(1<x<8), x+
x+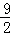 ),
),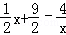 .
.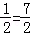 ,
,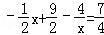 ,即2x2﹣11x+16=0(※)(9分)
,即2x2﹣11x+16=0(※)(9分) AB.(10分)
AB.(10分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
| A.长方形的周长确定,它的长与宽 |
| B.长方形的长确定,它的周长与宽 |
| C.长方形的面积确定,它的长与宽 |
| D.长方形的长确定,它的面积与宽 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,x与y的对应值如下表:
,x与y的对应值如下表:
 1 2 ﹣2 ﹣1 ﹣
1 2 ﹣2 ﹣1 ﹣ 的解为 ;不等式﹣x+1>﹣
的解为 ;不等式﹣x+1>﹣ 的解集为 .
的解集为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 和
和 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
| A.3 | B.4 | C. | D.5 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 上,点B在双曲线y=
上,点B在双曲线y= (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )
(k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com