
 和
和 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
| A.3 | B.4 | C. | D.5 |
 ),推出A的坐标和B的坐标,求出∠APB=90°,求出PA、PB的值,根据三角形的面积公式求出即可.
),推出A的坐标和B的坐标,求出∠APB=90°,求出PA、PB的值,根据三角形的面积公式求出即可. 上,
上, )(a为正数),
)(a为正数), 上,
上, ),
), ,
, 上,
上, =﹣
=﹣ ,
, ),
), ﹣(﹣
﹣(﹣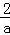 )|=
)|= ,PB=|a﹣(﹣2a)|=3a,
,PB=|a﹣(﹣2a)|=3a, PA×PB=
PA×PB= ×
× ×3a=
×3a= .
.

科目:初中数学 来源:不详 题型:填空题
 (度)与镜片焦距
(度)与镜片焦距 (米)成反比例.已知400度近视眼镜片的焦距为0.25米,则眼镜度数
(米)成反比例.已知400度近视眼镜片的焦距为0.25米,则眼镜度数 与镜片焦距
与镜片焦距 之间的函数关系式是______________.
之间的函数关系式是______________.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+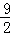 与双曲线y=
与双曲线y= (m>0)的交点.
(m>0)的交点.
 (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN= AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
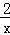 的图象如图所示,在同一直角坐标系内,如果将直线y=﹣x+1沿y轴向上平移2个单位后,那么所得直线与函数y=
的图象如图所示,在同一直角坐标系内,如果将直线y=﹣x+1沿y轴向上平移2个单位后,那么所得直线与函数y=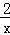 的图象的交点共有 _________ 个.
的图象的交点共有 _________ 个.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象上,则y1,y2,y3的大小关系是( )
的图象上,则y1,y2,y3的大小关系是( )| A.y3<y2<y1 | B.y2<y3<y1 |
| C.y1<y2<y3 | D.y1<y3<y2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
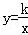 (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 (m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则
(m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则 = . (用含m的代数式表示)
= . (用含m的代数式表示)
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k值为 ( )
上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k值为 ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com