解:(1)由题意,A(0,1)、C(4,3)两点确定的直线解析式为:y=

x+1,
将点E的坐标(

,
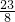
),代入y=

x+1中,左边=
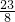
,右边=

×

+1=
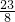
,
∵左边=右边,
∴点E在直线y=

x+1上,
即点A、C、E在一条直线上;
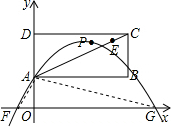
(2)连接GA、FA.
∵S
△GAO-S
△FAO=3
∴

GO•A0=

FO•AO=3.
∵OA=1,
∴GO-FO=6.
设F(x
1,0),G(x
2,0),
则x
1、x
2是方程ax
2+bx+1=0的两个根,且x
1<x
2,
又∵a<0
∴x
1•x
2=

<0,
∴GO=x
2、FO=-x
1∴x
2-(-x
1)=6,即x
2+x
1=6
∵x
2+x
1=-

,
∴-

=6,
∴抛物线的解析式为:y=ax
2-6ax+1,其顶点P的坐标为(3,1-9a)
∵顶点P在矩形ABCD的内部,
∴1<1-9a<3,
∴-

<a<0①
由方程组
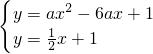
,
得:ax
2-(6a+

)x=0,
∴x=0或x=
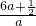
=6+

,
当x=0时,即抛物线与线段AE交于点A,而这条抛物线与线段AE有两个不同的交点,
则有:0<6+

<

,
解得:-

≤a<-

,
综合①②,得-

<a<-

,
∵b=-6a,
∴

<b<

.
分析:(1)说明点A、C、E在一条直线上,只要求出过A、C的直线的解析式,然后判断E是否满足函数的解析式就可以;
(2)连接GA、FA,已知△GAO与△FAO的面积差为3,而这两个三角形的高相同是OA的长,等于1,因而就可以得到OG与OF的长度的一个关系式.抛物线y=ax
2-6ax+1的顶点可以用a表示出来,顶点P在矩形ABCD的内部,即可以求出a的取值范围.
点评:本题综合运用了抛物线的顶点坐标的求法,以及一元二次方程的求解和韦达定理,及抛物线所经过的点,列方程组求a、b的值,难度较大.

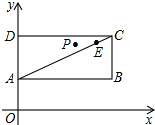 如图,已知点A(0,1),C(4,3),E
如图,已知点A(0,1),C(4,3),E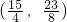 ,P是以AC为对角线的矩形ABCD内部(不在各边上)的一动点,点D在y轴上,抛物线y=ax2+bx+1以P为顶点.
,P是以AC为对角线的矩形ABCD内部(不在各边上)的一动点,点D在y轴上,抛物线y=ax2+bx+1以P为顶点. x+1,
x+1, ,
,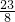 ),代入y=
),代入y= x+1中,左边=
x+1中,左边=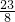 ,右边=
,右边= ×
× +1=
+1=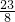 ,
, x+1上,
x+1上,
 GO•A0=
GO•A0= FO•AO=3.
FO•AO=3. <0,
<0, ,
, =6,
=6, <a<0①
<a<0①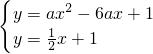 ,
, )x=0,
)x=0,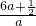 =6+
=6+ ,
, <
< ,
, ≤a<-
≤a<- ,
, <a<-
<a<- ,
, <b<
<b< .
.

 阅读快车系列答案
阅读快车系列答案 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设