
分析 (1)先将二次项系数化为1,然后再加上一次项系数$\frac{2}{3}$一半的平方.
(2)先将二次项系数化为1,然后再加上一次项系数一次项系数2一半的平方.
(3)先将二次项系数化为1,然后再加上一次项系数一次项系数-3一半的平方.
解答 解:(1)3x2+2x-2=3[x2+$\frac{2}{3}$x+($\frac{1}{3}$)2-($\frac{1}{3}$)2]-2=3(x+$\frac{1}{3}$)2-$\frac{7}{2}$.
故答案是:$\frac{1}{3}$;(-$\frac{7}{2}$);
(2)2y2+4y-3=2(y2+2y+1)-5=2(y+1)2-5.
故答案是:1;
(3)4x2-12x+15=4[x2-3x+($\frac{3}{2}$)2-($\frac{3}{2}$)2]+15=4(x-$\frac{3}{2}$)2+6.
故答案是:x-$\frac{3}{2}$.
点评 本题考查了配方方法的应用.解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为2.5吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系如图所示:
大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为2.5吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
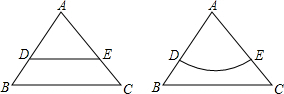 如果是两个全等的等边三角形ABC,平行于BC的线段DE与以点A为圆心的$\widehat{DE}$把△ABC的面积分成相等的两部分,则线段DE的长小于$\widehat{DE}$的长.(填“大于”“小于”或“等于”)
如果是两个全等的等边三角形ABC,平行于BC的线段DE与以点A为圆心的$\widehat{DE}$把△ABC的面积分成相等的两部分,则线段DE的长小于$\widehat{DE}$的长.(填“大于”“小于”或“等于”)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30πcm | B. | 30$\sqrt{2}$cm | C. | 15πcm | D. | 15$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
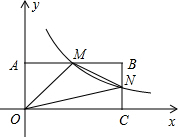 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com