
| A. | 30πcm | B. | 30$\sqrt{2}$cm | C. | 15πcm | D. | 15$\sqrt{2}$cm |
分析 画出圆锥展开图,设扇形的圆心角∠ASA′=n°,根据弧长公式得到$\frac{n•π•30}{180}$=2•π•$\frac{1}{2}$•15,解得n=90,则可判断△SAA′为等腰直角三角形,然后根据等腰直角三角形的性质求解.
解答 解:如图,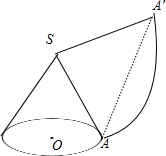 设扇形的圆心角∠ASA′=n°,
设扇形的圆心角∠ASA′=n°,
根据题意得$\frac{n•π•30}{180}$=2•π•$\frac{1}{2}$•15,解得n=90,
所以△SAA′为等腰直角三角形,
所以AA′=$\sqrt{2}$SA=30$\sqrt{2}$,
即彩带最少用30$\sqrt{2}$厘米.
故选B.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-a2)3=a6 | B. | (a+b)2=a2+b2 | C. | $\root{3}{-64}$=-4 | D. | 5$\sqrt{5}$-$\sqrt{5}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
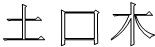 汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性,如图,三个汉字可以看成是轴对称图形.
汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性,如图,三个汉字可以看成是轴对称图形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是( )
如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com