
 大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为2.5吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系如图所示:
大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为2.5吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系如图所示:分析 (1)利用待定系数法求得销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系式,进一步代入x=300,求得y,进一步判定即可;
(2)利用销售利润=(销售单价×每公顷产量-每公顷成本)×公顷数列出函数解析式,利用配方法解答即可;
(3)利用(2)中求得的函数解析式与748建立方程求得答案即可.
解答 解:(1)设销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系式为y=kx+5,
代入(100,4.8)得k=-$\frac{1}{500}$,
则y=-$\frac{1}{500}$x+5,
当x=300时,y=-$\frac{1}{500}$×300+5=4.4,
补贴总金额是(4.5-4.4)×300×2.5=75(千元).
答:销售后享受政府补贴,则补贴总金额是75千元.
(2)由题意得W=2.5x(-$\frac{1}{500}$x+5)-8x=-$\frac{1}{200}$x2+4.5x=-$\frac{1}{200}$(x-450)2+1012.5.
即当x=450时,W取得最大值,也就是当种植面积为450公顷时,利润最大,最大利润是1012.5千元.
(3)①所得总利润不享受政府补贴时达到748千元,
由题意得-$\frac{1}{200}$x2+4.5x=748,
解得:x=220或x=680.
当x=220公顷时,y=4.56千元>4.5,不享受政府补贴;
当x=6800公顷时,y=3.64千元<4.5,享受政府补贴(舍去);
②所得总利润享受政府补贴时达到748千元,
当y=-$\frac{1}{500}$x+5=4.5时,x=250,
销售利润w=(4.5×2.5-8)x=748,解得x≈230<250(舍去);
答:应该种植220公顷公顷大豆.
点评 此题考查二次函数的性质及其应用,还考查抛物线的基本性质,另外将实际问题转化为求函数最值问题,从而来解决实际问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | y=0.2x+18.5(1≤x≤6) | B. | y=0.2x+18.7(1≤x≤6) | ||
| C. | y=0.2x+22(1≤x≤6) | D. | y=0.2x+22.2(1≤x≤6) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
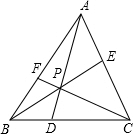 如图,在△ABC内任取一点P,连接并延长AP、BP、CP,分别交对边于点D、E、F,则$\frac{PD}{AD}$+$\frac{PE}{BE}$+$\frac{PF}{CF}$=1.
如图,在△ABC内任取一点P,连接并延长AP、BP、CP,分别交对边于点D、E、F,则$\frac{PD}{AD}$+$\frac{PE}{BE}$+$\frac{PF}{CF}$=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-a2)3=a6 | B. | (a+b)2=a2+b2 | C. | $\root{3}{-64}$=-4 | D. | 5$\sqrt{5}$-$\sqrt{5}$=4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com