
分析 设该药品平均每次提价的百分率为x,根据提价后的价格=降价前的价格(1+提价的百分率),则第一次提价后的价格是100(1+x),第二次后的价格是100(1+x)2,据此即可列方程求解
解答 解:设该药品平均每次提价的百分率为x,
根据题意得:100(1+x)2=144,
解得:x1=0.2,x2=-2.2,
经检验x2=-2.2不符合题意,
∴x=0.2=20%,
答:两次提价的百分率20%.
点评 本题考查了一元二次方程的应用.增长率问题:增长率=增长数量原数量×100%.如:若原数是a,每次增长的百分率为a,则第一次增长后为a(1+x);第二次增长后为a(1+x)2,即 原数×(1+增长百分率)2=后来数.


科目:初中数学 来源: 题型:解答题
 大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为2.5吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系如图所示:
大豆是一种非常受欢迎的农作物,已知种植某种大豆的平均产量为2.5吨/公顷,所需成本为8千元/公顷,某地销售大豆的单价y千元/吨与种植大豆的面积x公顷之间关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
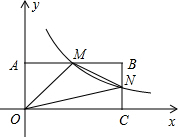 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥1 | B. | -4>x≤1 | C. | x<4 | D. | x≤1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com