
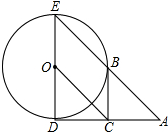
 如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙0于点B,且BC∥ED.
如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙0于点B,且BC∥ED.分析 (1)连接OB,由BC与OD平行,BC=OD,得到四边形BCDO为平行四边形,由AD为圆的切线,利用切线的性质得到OD垂直于AD,可得出四边形BCDO为矩形,利用矩形的性质得到OB垂直于BC,即可得出BC为圆O的切线;
(2)连接BD,由ED为圆O的直径,利用直径所对的圆周角为直角得到∠DBE为直角,由BCOE为平行四边形,得到BC与OE平行,且BC=OE=1,在直角三角形ABD中,C为AD的中点,利用斜边上的中线等于斜边的一半求出AD的长即可.
解答  解:(1)是,理由如下:
解:(1)是,理由如下:
如图,连接OB.
∵BC∥OD,DC=AC,∴BC=$\frac{1}{2}$DE=OD,
∴四边形BCDO为平行四边形,
∵AD为圆O的切线,
∴OD⊥AD,
∴四边形BCDO为矩形,
∴OB⊥BC,
则BC为圆O的切线;
(2)连接BD,∵DE是直径,
∴∠DBE=90°,
∵四边形BCOE为平行四边形,
∴BC∥OE,BC=OE=1,
在Rt△ABD中,C为AD的中点,
∴BC=$\frac{1}{2}$AD=1,
则AD=2.
点评 此题考查了切线的判定与性质,直角三角形斜边上的中线性质,以及平行四边形的判定与性质,熟练掌握切线的判定与性质是解本题的关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:填空题
 如图,长方形相框的外框的长是外框的宽的1.5倍,内框的长是内框的宽的2倍,外框与内框之间的宽度为3.设长方形相框的外框的长为x,外框的宽为y,则可所列方程组:$\left\{\begin{array}{l}{x=1.5y}\\{x-6=2(y-6)}\end{array}\right.$.
如图,长方形相框的外框的长是外框的宽的1.5倍,内框的长是内框的宽的2倍,外框与内框之间的宽度为3.设长方形相框的外框的长为x,外框的宽为y,则可所列方程组:$\left\{\begin{array}{l}{x=1.5y}\\{x-6=2(y-6)}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
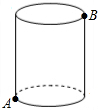 如图,有一圆柱,其高为8cm,它的底面半径为2cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为2$\sqrt{17}$ cm.(π取3)
如图,有一圆柱,其高为8cm,它的底面半径为2cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为2$\sqrt{17}$ cm.(π取3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
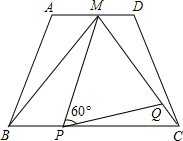 如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “两条线段可以组成一个三角形”是不确定事件 | |
| B. | “如果a≠0,那么(a+3)2=a2+32”是确定事件 | |
| C. | “同旁内角互补”是不确定事件 | |
| D. | “三角形三条角平分线交于一点”是确定事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com