
【题目】如图,这四边行ABCD中,点M、N分别在AB,CD边上,将四边形ABCD沿MN翻折,使点B、C分别在四边形外部点B1 , C1处,则∠A+∠B1+∠C1+∠D= . 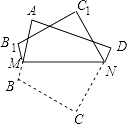
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为 . 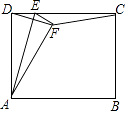
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax﹣1的图象与反比例函数y= ![]() 的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.
的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.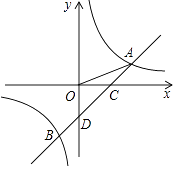
(1)求a,k的值及点B的坐标;
(2)直接写出不等式ax﹣1≥ ![]() 的解集;
的解集;
(3)在x轴上存在一点P,使得△POA与△OAC相似(不包括全等),请你求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
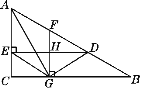
【题目】如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;
(3)若∠B=30°,判断四边形AEGF是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
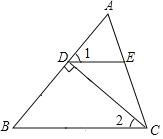
【题目】按要求完成下列证明:
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知),
∴∠1+ =90°( ).
∵∠1+∠2=90°(已知),
∴ =∠2( ).
∴DE∥BC( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
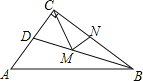
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
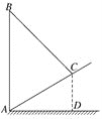
【题目】如图,是斜坡AC上的一根电线杆AB用钢丝绳BC进行固定的平面图.已知斜坡AC的长度为4 m,钢丝绳BC的长度为5 m,AB⊥AD于点A,CD⊥AD于点D,若CD=2 m,则电线杆AB的高度是多少.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米. 
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com