
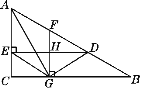
【题目】如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;
(3)若∠B=30°,判断四边形AEGF是否为菱形,并说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)四边形AEGF是菱形,理由见解析.
【解析】
(1)根据等腰三角形的性质及角平分线的定义可得∠CAG=∠FGA,即可证得AC∥FG;已知DE⊥AC,由此可得FG⊥DE,再由FG⊥BC可得 DE∥BC,所以AC⊥BC,从而得∠C=∠DHG=90°,∠CGE=∠GED;因为F是AD的中点,FG∥AE,可得H是ED的中点,所以FG是线段ED的垂直平分线,根据线段垂直平分线的性质可得GE=GD,所以∠GDE=∠GED,即可得∠CGE=∠GDE,利用AAS即可判定△ECG≌△GHD;(2)过点G作GP⊥AB于点P,易证△CAG≌△PAG,根据全等三角形的性质可得AC=AP,GC=GP;再证明Rt△ECG≌Rt△DPG,即可得EC=DP,由此即可证得结论;(3)四边形AEGF是菱形,根据已知条件易证AE=AF=FG,再由AE∥FG,即可判定四边形AEGF是菱形.
(1)证明:∵AF=FG,
∴∠FAG=∠FGA,
∵AG平分∠CAB,∴∠CAG=∠FAG,
∴∠CAG=∠FGA,∴AC∥FG.
∵DE⊥AC,∴FG⊥DE,
∵FG⊥BC,∴DE∥BC,∴AC⊥BC,
∴∠C=∠DHG=90°,∠CGE=∠GED,
∵F是AD的中点,FG∥AE,
∴H是ED的中点,
∴FG是线段ED的垂直平分线,
∴GE=GD,∴∠GDE=∠GED,
∴∠CGE=∠GDE,
∴△ECG≌△GHD.
(2)证明:过点G作GP⊥AB于点P,如图.
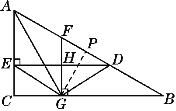
∴GC=GP,∴△CAG≌△PAG,
∴AC=AP,GC=GP.
由(1)得GE=GD,
∴Rt△ECG≌Rt△DPG,
∴EC=DP,
∴AD=AP+PD=AC+EC.
(3)解:四边形AEGF是菱形,理由如下:
∵∠B=30°,∴∠ADE=30°,
∴AE=![]() AD,∴AE=AF=FG,
AD,∴AE=AF=FG,
由(1)得AE∥FG,
∴四边形AEGF是菱形.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】计算题|1﹣ ![]() |﹣
|﹣ ![]() +2cos30°﹣20170;
+2cos30°﹣20170;
(1)计算:|1﹣ ![]() |﹣
|﹣ ![]() +2cos30°﹣20170;
+2cos30°﹣20170;
(2)解不等式组 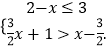 并求其最小整数解.
并求其最小整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
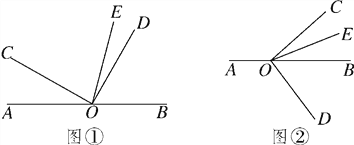
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )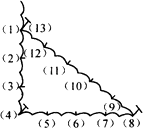
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.如果三角形两条边长的平方和等于第三边长的平方
D.如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这四边行ABCD中,点M、N分别在AB,CD边上,将四边形ABCD沿MN翻折,使点B、C分别在四边形外部点B1 , C1处,则∠A+∠B1+∠C1+∠D= . 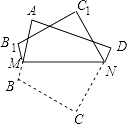
查看答案和解析>>
科目:初中数学 来源: 题型:
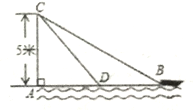
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点的左边,距离原点8个单位长度,点B在原点的右边.
(Ⅰ)求点A,点B对应的数;
(Ⅱ)数轴上点A以每秒1个单位长度出发向左移动,同时点B以每秒3个单位长度的速度向左移动,在点C处追上了点A,求点C对应的数.
(Ⅲ)已知在数轴上点M从点A出发向右运动,速度为每秒1个单位长度,同时点N从点B出发向右运动,速度为每秒2个单位长度,设线段NO的中点为P(O为原点),在运动的过程中,线段![]() 的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a>b,选择适当的不等号填空:
(1)-![]() ________-
________-![]() ;
;
(2)1-5a__________1-5b;
(3)ax2_________bx2;
(4)a(-c2-1)_________b(-c2-1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com