
 如图,C是线段BD上一点,△ABC与△CDE为BD同侧的等边三角形,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形共有3对,分别是△BCE与△ACD,△BCG与△ACF、△CDF与△CEG.
如图,C是线段BD上一点,△ABC与△CDE为BD同侧的等边三角形,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形共有3对,分别是△BCE与△ACD,△BCG与△ACF、△CDF与△CEG. 分析 根据等边三角形的性质得CB=CA,CE=CD,∠BCA=∠DCE=60°,根据旋转的定义,把△BCE绕点C顺时针旋转60°可得到△ACD,再根据旋转的性质得∠CBE=∠CAD,∠BEC=∠ADC,再证明△CDF≌△CEG得到CF=CG,于是根据旋转的定义,把△CDF绕点C逆时针旋转60°可得到△CEG,同样可得△BCG绕点C顺时针旋转60°可得到△ACF.
解答 解:∵△ABC与△CDE为等边三角形,
∴CB=CA,CE=CD,∠BCA=∠DCE=60°,
∴△BCE绕点C顺时针旋转60°可得到△ACD,
∴∠CBE=∠CAD,∠BEC=∠ADC,
在△CDF和△CEG中,
$\left\{\begin{array}{l}{∠CDF=∠CEG}\\{CD=CE}\\{∠DCF=∠ECG}\end{array}\right.$,
∴△CDF≌△CEG,
∴CF=CG,
∴△CDF绕点C逆时针旋转60°可得到△CEG,
同样可得△BCG绕点C顺时针旋转60°可得到△ACF.
故答案为△CDF与△CEG.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=-x2+(m-1)x+m(m为常数)的图象与y轴交于点(0,3)
已知二次函数y=-x2+(m-1)x+m(m为常数)的图象与y轴交于点(0,3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 南偏东46° | B. | 东偏北46° | C. | 东偏南46° | D. | 南偏东44° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示:残缺的圆形轮片上,弦AB的垂直平分线CD交圆形轮片于点C,垂足为D,解答下列问题:
如图所示:残缺的圆形轮片上,弦AB的垂直平分线CD交圆形轮片于点C,垂足为D,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
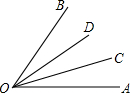 如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.
如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
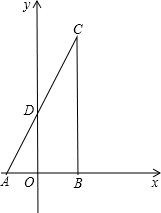 已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,
已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com