
如图,已知A、B两点的坐标分别为A(0,2 ),B(2,0)直线AB与反比例函数
),B(2,0)直线AB与反比例函数 的图象交与点C和点D(-1,a).
的图象交与点C和点D(-1,a).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数.
(1)直线AB解析式为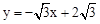 ,反比例解析式为
,反比例解析式为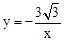 ;(2)30°.
;(2)30°.
解析试题分析:(1)设直线AB的解析式为y=kx+b(k≠0),将A与B坐标代入求出k与b的值,确定出直线AB的解析式,将D坐标代入直线AB解析式中求出a的值,确定出D的坐标,将D坐标代入反比例解析式中求出m的值,即可确定出反比例解析式;(2)联立两函数解析式求出C坐标,过C作CH垂直于x轴,在直角三角形OCH中,由OH与HC的长求出tan∠COH的值,利用特殊角的三角函数值求出∠COH的度数,在三角形AOB中,由OA与OB的长求出tan∠ABO的值,进而求出∠ABO的度数,由∠ABO-∠COH即可求出∠ACO的度数.
试题解析:(1)设直线AB的解析式为y=kx+b(k≠0),
将A(0,2 ),B(2,0)代入得:
),B(2,0)代入得: ,解得:
,解得: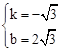 .
.
∴直线AB解析式为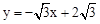 .
.
将D(-1,a)代入直线AB解析式得: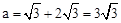 ,则D(-1,
,则D(-1,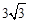 ).
).
将D坐标代入 中,得:m=
中,得:m=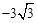 .
.
∴反比例解析式为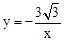 .
.
(2)联立两函数解析式得: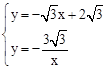 ,解得:
,解得: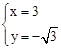 或
或 .
.
∴C坐标为(3,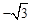 ).
).
过点C作CH⊥x轴于点H,
在Rt△OHC中,CH= ,OH=3,
,OH=3,
∴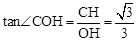 .∴∠COH=30°.
.∴∠COH=30°.
在Rt△AOB中,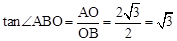 ,∴∠ABO=60°.
,∴∠ABO=60°.
∴∠ACO=∠ABO-∠COH=30°.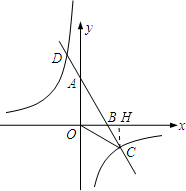
考点:1.反比例函数与一次函数的交点问题;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4. 锐角三角函数定义;5.特殊角的三角函数值.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
某公司准备与汽车租赁公司签订租车合同.以每月用车路程x(km)计算,甲汽车租赁公司的月租费 元,乙汽车租赁公司的月租费是
元,乙汽车租赁公司的月租费是 元.如果
元.如果 、
、 与x之间的关系如图所示.
与x之间的关系如图所示.
(1)求 、
、 与x之间的函数关系
与x之间的函数关系
(2)怎样选用汽车租赁比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,函数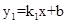 的图象与函数
的图象与函数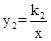 (
(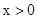 )的图象交于点A(2,1)、B,与y轴交于点C(0,3).
)的图象交于点A(2,1)、B,与y轴交于点C(0,3).
(1)求函数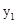 的表达式和点B的坐标;
的表达式和点B的坐标;
(2)观察图象,比较当x>0时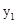 与
与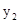 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水 吨,应交水费
吨,应交水费 元.
元.
(1)若0< ≤6,请写出
≤6,请写出 与
与 的函数关系式.(3分)
的函数关系式.(3分)
(2)若 >6,请写出
>6,请写出 与
与 的函数关系式.(3分)
的函数关系式.(3分)
(3)在同一坐标系下,画出以上两个函数的图象.(4分)
(4)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知反比例函数 的图象与一次函数
的图象与一次函数 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B
( ,
, ).
).
(1)求这两个函数的表达式;
(2)观察图象,当 >0时,直接写出
>0时,直接写出 >
>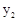 时自变量
时自变量 的取值范围;
的取值范围;
(3)如果点C与点A关于 轴对称,求△ABC的面积.
轴对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).
(1)如图1,当点C与点O重合时,求直线BD的解析式;
(2)如图2,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的⊙B与y轴相切(切点为C)时,求点B的坐标;
(3)如图3,点C从点O沿y轴向下移动,当点C的坐标为C 时,求∠ODB的正切值.
时,求∠ODB的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获得利润100元,每生产一个乙种产品可获得利润180元.在这10名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品.
(1)请写出此车间每天获取利润y(元)与x(人)之间的函数关系式;
(2)若要使此车间每天获取利润为14400元,要派多少名工人去生产甲种产品?
(3)若要使此车间每天获取利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.当容器内的水量大于5升时,求时间x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com