
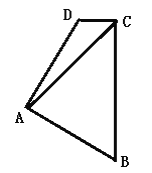
【题目】如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=900,连结AC,若AC=10,则四边形ABCD的面积为_____.
【答案】50
【解析】
作辅助线;证明△ABM≌△ADN,得到AM=AN,△ABM与△ADN的面积相等;求出正方形AMCN的面积即可解决问题.
解:如图,作AM⊥BC、AN⊥CD,交CD的延长线于点N;
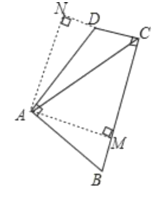
∵∠BAD=∠BCD=90°
∴四边形AMCN为矩形,∠MAN=90°;
∵∠BAD=90°,
∴∠BAM=∠DAN;
在△ABM与△ADN中,
∠BAM=∠DAN
∠AMB=∠AND
AB=AD,
∴△ABM≌△ADN(AAS),
∴设AM=AN=m;
∵△ABM与△ADN的面积相等;
∴四边形ABCD的面积=正方形AMCN的面积;
由勾股定理得:AC2=AM2+MC2,而AC=10;
∴2m2=100,m2=50,
故答案为:50.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y= ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】藏族小伙小游到批发市场购买牛肉,已知牦牛肉和黄牛肉的单价之和为每千克44元,小游准备购买牦牛肉和黄牛肉总共不超过120千克,其中黄牛肉至少购买30千克,牦牛肉的数量不少于黄牛肉的2倍,粗心的小游在做预算时将牦牛肉和黄牛肉的价格弄对换了,结果实际购买两种牛肉的总价比预算多了224元,若牦牛肉、黄牛肉的单价和数量均为整数,则小游实际购买这两种牛肉最多需要花费______元![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 的坐标是
的坐标是![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,在
,在![]() 轴正半轴上截取
轴正半轴上截取![]() ,连接
,连接![]() .
.
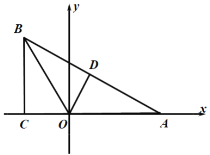
(1)求![]() 点的坐标及
点的坐标及![]() 的解析式;
的解析式;
(2)过![]() 作
作![]() 于
于![]() ,求证:
,求证:![]() ;
;
(3)![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,在
,在![]() 上取
上取![]() 点,连接
点,连接![]() ,动点
,动点![]() 沿
沿![]() 运动,
运动,![]() 在
在![]() 上的运动速度每秒1个单位长度,
上的运动速度每秒1个单位长度,![]() 在
在![]() 上运动速度每秒2个单位长度,当
上运动速度每秒2个单位长度,当![]() 在何处时,
在何处时,![]() 运动的时间最短?请求出
运动的时间最短?请求出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出![]() 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.

(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() 图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为3,则k的值为( )
图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为3,则k的值为( )

A. 3 B. 6 C. 4 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B﹣C﹣D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现:已知△ABC中,AE是△ABC的角平分线,∠B=72°,∠C=36°
(1)如图1,若AD⊥BC于点D,求∠DAE的度数;
(2)如图2,若P为AE上一个动点(P不与A、E重合),且PF⊥BC于点F时,∠EPF= °.
(3)探究:如图2△ABC中,已知∠B,∠C均为一般锐角,∠B>∠C,AE是△ABC的角平分线,若P为线段AE上一个动点(P不与E重合),且PF⊥BC于点F时,请写出∠EPF与∠B,∠C的关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com