
����Ŀ����ͼ������ABC����DEF���ǵ���ֱ�������Σ���ACB=��EDF=90�㣬�ҵ�D��AB���ϣ�AB��EF���е��ΪO������BF��CD��CO����Ȼ��C��F��O��ͬһ��ֱ���ϣ�����֤����BOF�ա�COD����BF=CD��
�������
��1����ͼ���е�Rt��DEF�Ƶ�O��ת�õ�ͼ���������ʱ�߶�BF��CD��������ϵ����֤����Ľ��ۣ�
��2����ͼ��������ABC����DEF���ǵȱ������Σ�AB��EF���е��ΪO��������1���еĽ�����Ȼ�����������������˵�����ɣ��粻�����������BF��CD֮���������ϵ��
��3����ͼ��������ABC����DEF���ǵ��������Σ�AB��EF���е��Ϊ0���Ҷ�����ACB=��EDF=������ֱ��д��![]() ��ֵ���ú�����ʽ�ӱ�ʾ������
��ֵ���ú�����ʽ�ӱ�ʾ������

���𰸡���1�� BF=CD��֤������������2����1���еĽ��۲����������ɼ���������3��![]() =tan
=tan![]() ��
��
��������
�����������1�����ͼ����ʾ������OC��OD��֤����BOF�ա�COD��
��2�����ͼ����ʾ������OC��OD��֤����BOF�ס�COD�����Ʊ�Ϊ![]() ��
��
��3�����ͼ����ʾ������OC��OD��֤����BOF�ס�COD�����Ʊ�Ϊtan![]() ��
��
�����������1�����룺BF=CD���������£�
���ͼ����ʾ������OC��OD��
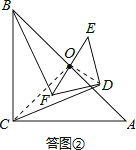
�ߡ�ABCΪ����ֱ�������Σ���OΪб��AB���е㣬
��OB=OC����BOC=90����
�ߡ�DEFΪ����ֱ�������Σ���OΪб��EF���е㣬
��OF=OD����DOF=90����
�ߡ�BOF=��BOC+��COF=90��+��COF����COD=��DOF+��COF=90��+��COF��
���BOF=��COD��
������BOF����COD��

���BOF�ա�COD��SAS����
��BF=CD��
��2������1���еĽ��۲�������
���ͼ����ʾ������OC��OD��
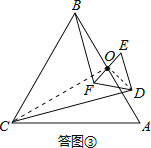
�ߡ�ABCΪ�ȱ������Σ���OΪ��AB���е㣬
��![]() =tan30��=
=tan30��=![]() ����BOC=90����
����BOC=90����
�ߡ�DEFΪ�ȱ������Σ���OΪ��EF���е㣬
��![]() =tan30��=
=tan30��=![]() ����DOF=90����
����DOF=90����
��![]() ��
��
�ߡ�BOF=��BOC+��COF=90��+��COF����COD=��DOF+��COF=90��+��COF��
���BOF=��COD��
����BOF����COD��
��![]() ����BOF=��COD��
����BOF=��COD��
���BOF�ס�COD��
��![]()
��3�����ͼ����ʾ������OC��OD��
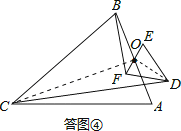
�ߡ�ABCΪ���������Σ���OΪ�ױ�AB���е㣬
��![]() =tan
=tan![]() ����BOC=90����
����BOC=90����
�ߡ�DEFΪ���������Σ���OΪ�ױ�EF���е㣬
��![]() =tan
=tan![]() ����DOF=90����
����DOF=90����
��![]() =
=![]() =tan
=tan![]()
�ߡ�BOF=��BOC+��COF=90��+��COF����COD=��DOF+��COF=90��+��COF��
���BOF=��COD��
����BOF����COD��
��![]() =
=![]() =tan
=tan![]() ����BOF=��COD��
����BOF=��COD��
���BOF�ס�COD��
��![]() =tan
=tan![]() ��
��


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ͳ�����У���ʾһ��������ɢ�̶ȵ�����( )
A.ƽ����B.����C.����D.��λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������̹�����15̨���˻�е��ÿ̨��еÿСʱ������3 m3������2 m3.Ϊ��ʹ�����Ĺ����������Ĺ���ͬʱ���������谲����x̨��е��������xӦ����ķ�����( )
A. 2x��3(15��x) B. 3x��2(15��x)
C. 15��2x��3x D. 3x��2x��15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��3����1������ԭ��ĶԳƵ�A���������ǣ� ��
A.����3����1��B.��3��1��C.����3��1��D.����1��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊ1��С��������ɵ������������н�����ͼƬ��ʾ��ƽ��ֱ������ϵ����֪���������ABC�������ε��������㶼��С�������ϣ� 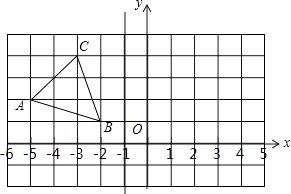
��1��������ABC����ֱ��l��x=��1�ĶԳ������Ρ�A1B1C1����д��A1��B1��C1�����꣮
��2����ֱ��x=��l����һ��D��ʹBD+CD��С������������D��Ϊ ��
��ʾ��ֱ��x=��l�ǹ��㣨��1��0���Ҵ�ֱ��x���ֱ�ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2014�괺����ʼ������ũ��ʵ���������༯�д�������ũ�廷�������ۺ����Σ����������ǵļ�������ij��Ҫ����һ�����������ڵ����������üס����������ͣ���������15�˿���ɣ���֪�ס���������������˶��������ҳ����������Ǽ׳���3������ס���������������˶����������˶����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����|a|��|b|����a��b�Ĺ�ϵ��( )
A. ��� B. ��Ϊ�෴�� C. ��Ȼ�Ϊ�෴�� D. ���ж�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com