
【题目】在平面直角坐标系中,已知点A![]() ,点B
,点B![]() ,点C是y轴上的一个动点,当∠BCA=30°时,点C的坐标为______.
,点C是y轴上的一个动点,当∠BCA=30°时,点C的坐标为______.
【答案】(0,![]() ),(0,
),(0,![]() )
)
【解析】
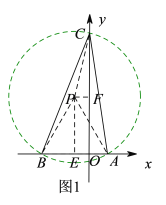
(1)如图1,以AB为边在x轴的上方作等边△PAB,再以点P为圆心,PA为半径作圆P,交y轴的正半轴于点C,连接BC、AC,则此时∠BCA=30°,再根据题中的已知条件求得线段OC的长,即可得到此时点C的坐标;
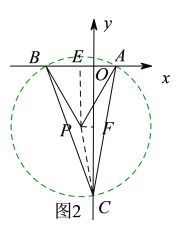
(2)如图2,和(1)同理在y轴的负半轴可求得另一个符合要求的点C的坐标.
(1)如图1,以AB为边在x轴的上方作等边△PAB,则∠APB=60°,再以点P为圆心,PA为半径作圆P,交y轴的正半轴于点C,连接BC、AC,则此时由∠APB=60°可得∠BCA=30°,
∵点A、B的坐标分别为:![]() ,
,![]() ,
,
∴AB=![]() ,OB=
,OB=![]()
∴PA=PC=AB=![]() ,
,
过点P作PF⊥y轴于点F,PE⊥x轴于点E,则四边形PEOF是矩形,
∴OF=PE,PF=OE,
∵在等边△PAB中,PE=PA·sin60°=![]() ,BE=
,BE=![]() AB=
AB=![]() ,
,
∴OF=12,OE=OB-BE=![]() ,
,
∴PF=![]() ,
,
又∵在Rt△PFC中,PC=![]() ,∠PFC=90°,
,∠PFC=90°,
∴CF=![]() ,
,
∴OC=OF+CF=![]() ,
,
∴此时点C的坐标为![]() ;
;
(2)如图2,以AB为边在x轴的下方作等边△PAB,则∠APB=60°,再以点P为圆心,PA为半径作圆P,交y轴的负半轴于点C,连接BC、AC,则此时由∠APB=60°可得∠BCA=30°,和(1)同理可得此时点C的坐标为:![]() ;
;
综上所述,符合条件的点C的坐标为![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.

(1)求证:四边形DEBF是菱形;
(2)请判断四边形AGBD是什么特殊四边形? 并加以证明;
(3)若AD=1,求四边形AGCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽“的勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a、b,那么![]() 的值为( ).
的值为( ).

A. 49 B. 25 C. 13 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
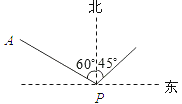
【题目】如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向.求货船的航行速度.(精确到0.1海里/时,参考数据:![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
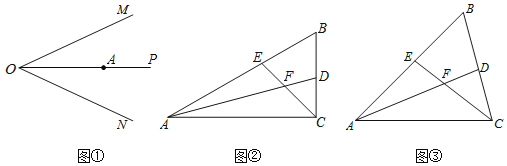
【题目】(1)如图①,OP是∠MON的平分线,点A为OP上一点,请你作一个∠BAC,B、C分别在OM、ON上,且使AO平分∠BAC(保留作图痕迹);
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,△ABC的平分线AD,CE相交于点F,请你判断FE与FD之间的数量关系(可类比(1)中的方法);
(3)如图③,在△ABC中,如果∠ACB≠90°,而(2)中的其他条件不变,请问(2)中所得的结论是否仍然成立?若成立,请证明,若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
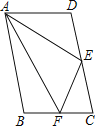
【题目】如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com