
【题目】一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的价位为y万元,则y关于x的函数关系式为( )
A.y=60(1﹣x)2
B.y=60(1﹣x2)
C.y=60﹣x2
D.y=60(1+x)2
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.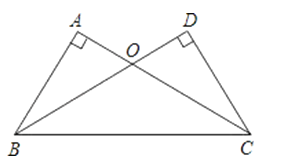
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示,根据图中的信息,回答问题: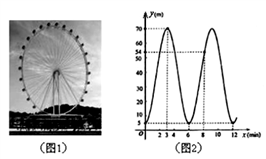
(1)根据图2补全表格:
(2)如表反映的两个变量中,自变量是 , 因变量是;
(3)根据图象,摩天轮的直径为m,它旋转一周需要的时间为min.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名的瑞士数学家欧拉曾指出:可以表示为四个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为四个整数平方之和,即 ![]()
![]() ,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可概括为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可概括为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
【阅读思考】
在数学思想中,有种解题技巧称之为“无中生有”.例如问题:将代数式 ![]() 改成两个平方之差的形式.解:原式
改成两个平方之差的形式.解:原式 ![]() ﹒
﹒
(1)【动手一试】试将 ![]() 改成两个整数平方之和的形式. (12+52)(22+72)=;
改成两个整数平方之和的形式. (12+52)(22+72)=;
(2)【解决问题】请你灵活运用利用上述思想来解决“不变心的数”问题:将代数式 ![]() 改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.
(1)图中共有几对全等三角形,请把它们都写出来;
(2)求证:∠MAE=∠NCF.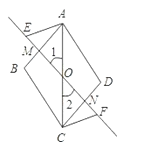
查看答案和解析>>
科目:初中数学 来源: 题型:
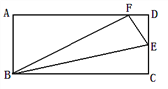
【题目】(本题9分)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE
(2)若△BEF也与△ABF相似,请求出![]() 的值 .
的值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com