
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.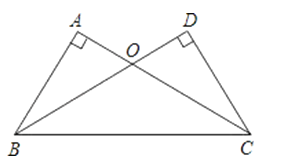
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】下列叙述中不正确的是( )
A. 圆是中心对称图形,圆心是它的对称中心B. 圆是轴对称图形,直径是它的对称轴
C. 连接圆上两点的线段叫弦D. 圆上两点间的部分叫弧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)指定路灯的位置(用点P表示);
(2)在图中画出表示大树高的线段(用线段MG表示);
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.
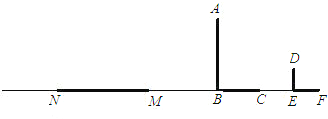
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某军事行动中,对军队部署的方位,采用钟代码的方式来表示、例如,北偏东30°方向45千米的位置,与钟面相结合,以钟面圆心为基准,时针指向北偏东30°的时刻是1:00,那么这个地点就用代码010045来表示、按这种表示方式,南偏东40°方向78千米的位置,可用代码表示为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】收集和整理数据.
某中学七(1)班学习了统计知识后,数学老师要求每个学生就本班学生的上学方式进行一次全面调查,如图是一同学通过收集数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题:(每个学生只选择1种上学方式).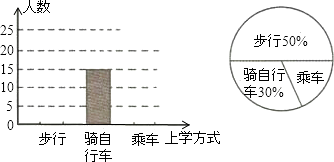
(1)求该班乘车上学的人数;
(2)将频数分布直方图补充完整;
(3)若该校七年级有1200名学生,能否由此估计出该校七年级学生骑自行车上学的人数,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一台机器原价60万元,如果每年的折旧率为x,两年后这台机器的价位为y万元,则y关于x的函数关系式为( )
A.y=60(1﹣x)2
B.y=60(1﹣x2)
C.y=60﹣x2
D.y=60(1+x)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com