练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在平面直角坐标系中，已知反比例函数y=(x>0)的图象和菱形OABC，且OB=4，tan∠BOC=，若将菱形向右平移，菱形的两个顶点B、C恰好同时落在反比例函数的图象上，则反比例函数的解析式是______________.

    【答案】

    【解析】

    解：连接AC，交y轴于D．∵四边形形OABC是菱形，∴AC⊥OB，OD=BD，AD=CD．∵OB=4，tan∠BOC=，∴OD=2，CD=1，∴A（﹣1，2），B（0，4），C（1，2）．设菱形平移后B的坐标是（x，4），C的坐标是（1+x，2）．∵B、C落在反比例函数的图象上，∴k=4x=2（1+x），解得：x=1，即菱形平移后B的坐标是（1，4），代入反比例函数的解析式得：k=1×4=4，即B、C落在反比例函数的图象上，菱形的平移距离是1，反比例函数的解析式是y=．故答案为：y=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】学校为了解全校1600名学生到校上学的方式，在全校随机抽取了若干名学生进行问卷调查．问卷给出了五种上学方式供学生选择，每人只能选一项，且不能不选．将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图（均不完整）．

    （1）问：在这次调查中，一共抽取了多少名学生？

    （2）补全频数分布直方图；

    （3）估计全校所有学生中有多少人乘坐公交车上学．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正比例函数y=kx（k＞0）的图象与x轴相交所成的锐角为70°，定点A的坐标为（0，8），P为y轴上的一个动点，M、N为函数y=kx（k＞0）的图象上的两个动点，则AM+MP+PN的最小值为（　　）

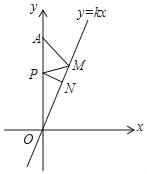
    A. 4 B. 4 C. 8sin40° D. 8sin20°（1+cos20°+sin20°cos20°）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时费按y元/分钟计算（总费用不足9元按9元计价）．小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：

    时间（分钟）

    里程数（公里）

    车费（元）

    小明

    8

    8

    12

    小刚

    12

    10

    16

    （1）求x，y的值；

    （2）如果小华也用该打车方式，打车行驶了11公里，用了14分钟，那么小华的打车总费用为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知抛物线y=ax2+bx（a≠0）经过A（6，0）、B（8，8）两点．

    （1）求抛物线的解析式；

    （2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m的值及点D的坐标；

    （3）如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，在坐标平面内有点P，求出所有满足△POD∽△NOB的点P坐标（点P、O、D分别与点N、O、B对应）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题：探究函数的图象与性质．小华根据学习函数的经验，对函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：在函数y＝|x|﹣2中，自变量x可以是任意实数；

    Ⅰ如表是y与x的几组对应值．

    y

    …

    ﹣3

    ﹣2

    ﹣1

    0

    1

    2

    3

    …

    x

    …

    1

    0

    ﹣1

    ﹣2

    ﹣1

    0

    m

    …

    ①m＝　 　；

    ②若A（n，8），B（10，8）为该函数图象上不同的两点，则n＝　 　；

    Ⅱ如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；根据函数图象可得：

    ①该函数的最小值为　 　；

    ②该函数的另一条性质是　 　．

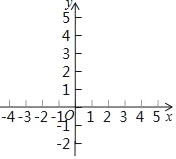
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD．

    （1）求证：四边形ACED是平行四边形；

    （2）若AC=2，CE=4，求四边形ACEB的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)请画出△ABC关于y轴对称的△A'B'C'(其中A'，B'，C'分别是A，B，C的对应点，不写画法).

    (2)直接写出A′，B′，C'三点的坐标：A'_______，B'______，C'______；

    (3)△ABC的面积为_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°．

    （1）判断∠D是否是直角，并说明理由．

    （2）求四边形ABCD的面积.

    查看答案和解析>>

    同步练习册答案