练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
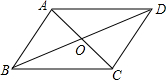
    14．?ABCD中，对角线AC与BD交于点O，∠DAC=42°，∠CBD=23°，则∠COD是（　　）
    A．61°B．63°C．65°D．67°

    分析 由平行四边形的性质可知：AD∥BC，进而可得∠DAC=∠BCA，再根据三角形外角和定理即可求出∠COD的度数．

    解答 解：∵四边形ABCD是平行四边形，
    ∴AD∥BC，
    ∴∠DAC=∠BCA=42°，
    ∴∠COD=∠CBD+∠BCA=65°，
    故选C．

    点评 本题考查了平行四边形的性质以及三角形的外角和定理，题目比较简单，解题的关键是灵活运用平行四边形的性质，将四边形的问题转化为三角形问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．4个数a，b，c，d排列成$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$，我们称之为二阶行列式．规定它的运算法则为：$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc．若$|\begin{array}{l}{x+3}&{x-3}\\{x-3}&{x+3}\end{array}|$=12，则x=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．解不等式：4（x-1）＞5x-6，并把它的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

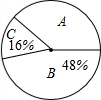    2．某班数学老师想了解学生对数学的喜欢程度，对全班50名学生进行调查，根据调查结果绘制了扇形统计图（如图所示），其中A表示“很喜欢”，B表示“一般”，C表示“不喜欢”，则该班“很喜欢”数学的学生有18人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，四边形ABCD是⊙O的内接四边形，∠B=70°，则∠D的度数是（　　）
    A．110°B．90°C．70°D．50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．雾霾天气严重影响市民的生活质量．在今年寒假期间，某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民．并对调查结果进行了整理．绘制了如图不完整的统计图表．观察分析并回答下列问题．

    （1）本次被调查的市民共有多少人？
    （2）分别补全条形统计图和扇形统计图，并计算图2中区域B所对应的扇形圆心角的度数；
    （3）若该市有100万人口，请估计持有A、B两组主要成因的市民有多少人？
    组别雾霾天气的主要成因百分比
    A工业污染45%
    B汽车尾气排放m
    C炉烟气排放15%
    D其他（滥砍滥伐等）n

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的图象刻画了“龟兔再次赛跑”的故事（x表示乌龟从起点出发所行的时间，y1表示乌龟所行的路程，y2表示兔子所行的路程）．下列说法错误的是（　　）
    A．“龟兔再次赛跑”的路程为1000米B．兔子和乌龟同时从起点出发
    C．乌龟在途中休息了10分钟D．兔子在途中750米处追上乌龟

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．【结论】已知两条直线L1：y=k1x+b1，L2：k2x+b2，若L1⊥L2，则有k1•k2=-1，反之也成立．
    【应用】（1）已知y=3x+1与y=kx-1垂直，求k及它们的交点坐标；
    （2）已知直线M经过点A（2，3），且与y=-$\frac{1}{2}$x+3垂直，求直线M的解析式．
    【探究】（3）在同一直角坐标系上，给定4个点A（1，3）、B（-3，0）、C（0，-4）和D（4，-1），任意连接其中两点能得到多少条不同的直线？这些直线中共有多少组互相垂直关系？并选择其中一组互相垂直关系进行证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图所示，已知∠1=52°，∠2=52°，∠3=91°，那么∠4=89．

    查看答案和解析>>

    同步练习册答案