
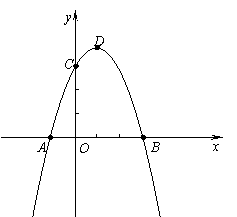
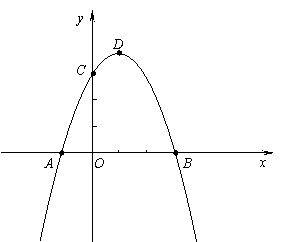
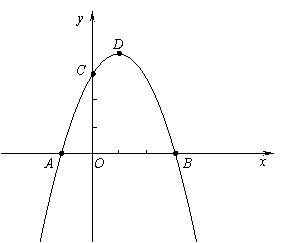
如图, 在平面直角坐标系中,二次函数
在平面直角坐标系中,二次函数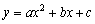 (
(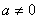 )的图象经过点A(-1,0)、
)的图象经过点A(-1,0)、
点B(3,0)、点C(0,3).
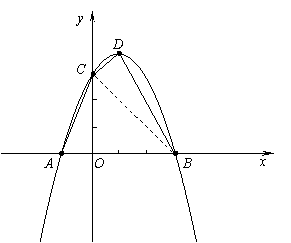
(1)求此抛物线的解析式及顶点D的坐标;
(2)连结AC、CD、BD,试比较∠BCA与∠BDC的大小,并说明理由;
 (3)若在x轴上有一动点M,在抛物线
(3)若在x轴上有一动点M,在抛物线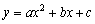 上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
|
 解:(1)∵点A、B、C在抛物线
解:(1)∵点A、B、C在抛物线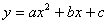 上,
上,
∴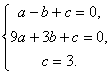 解得
解得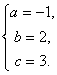
∴此抛物线为: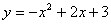 ………2分
………2分
由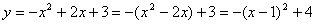
∴抛物线的顶点D的坐标为(1,4). ………4分
(2)连结BC,
由点C(0,3)、B(3,0)、D(1,4)
 可得CD=
可得CD=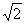 ,BD=
,BD=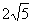 ,CB=
,CB=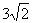
由点C(0,3)、A(-1,0),可得AC=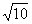
由
∴△CDB∽△OAC ∴∠BCA=∠BDC ………8分
(3)设点M的坐标为(t,0)
则由C(0,3)、B(3,0)、M(t,0)可以得到
若能构成平行四边形时点N的坐标有三种可能,
 分别是(3-t,3),(t-3,3),(t+3,-3)
分别是(3-t,3),(t-3,3),(t+3,-3)
∵点N在抛物线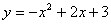 上
上
当把(3-t,3)代入时,
可得t=1或t=3(点M与点B重 合,舍去);
合,舍去);
当把(t-3,3)代入时,
可得t=5或t=3(点M与点B重合,舍去);
当把(t+3,-3)代入时,
可得t=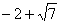 或t=
或t=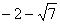 ,
,
综上可知,M的坐标为(1,0)、(5,0)、(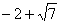 ,0)、(
,0)、(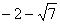 ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
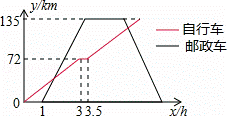
为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途径乙地短暂休息完成补给后,继续骑行至目的地丙地,自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地,自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的2.5倍,如图表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的函数关系图象,请根据图象提供的信息解答下列各题:
(1)自行车队行驶的速度是 km/h;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5.
(1)用“直尺和圆规”在BC边上找一点O,使以点O为圆心,OC为半径的圆与AB相切,并画出⊙O(保留作图痕迹,不写作法);
(2)求(1)中所画圆的半径.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
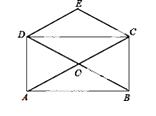
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长 ( )
|
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
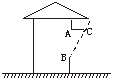
如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8 m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为 ( )
A、1.8tan80°m B、1.8cos80°m C、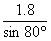 m D、
m D、 m
m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com