
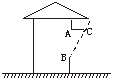
如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8 m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为 ( )
A、1.8tan80°m B、1.8cos80°m C、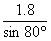 m D、
m D、 m
m
 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
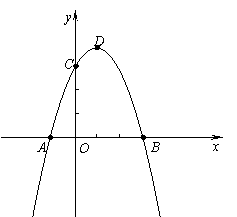
如图, 在平面直角坐标系中,二次函数
在平面直角坐标系中,二次函数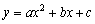 (
(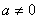 )的图象经过点A(-1,0)、
)的图象经过点A(-1,0)、
点B(3,0)、点C(0,3).
(1)求此抛物线的解析式及顶点D的坐标;
(2)连结AC、CD、BD,试比较∠BCA与∠BDC的大小,并说明理由;
 (3)若在x轴上有一动点M,在抛物线
(3)若在x轴上有一动点M,在抛物线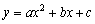 上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
|
查看答案和解析>>
科目:初中数学 来源: 题型:
升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时该同学视线的仰角恰为30°,若双眼离地面1.5米,则旗杆的高度为______米.(用含根号的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
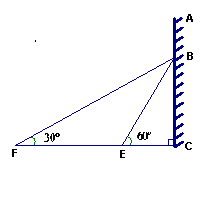
如图,为迎接中国---东盟博览会,在某建筑物AC上,挂着一宣传条幅BC,小明站在点F处,看条幅顶端B,测的仰角为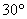 ,再往条幅方向前
,再往条幅方向前 行20米到达点E处,,看到条幅顶端B,测的仰角为
行20米到达点E处,,看到条幅顶端B,测的仰角为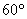 ,求宣传条幅BC的长,(小明的身高不计,结果精确到0.1米)
,求宣传条幅BC的长,(小明的身高不计,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
下列各式中,正确的是( )
A、sin200+sin300=sin500; B、sin600=2sin300;
C、tan200﹒t an700=1; D、cos300<cos600;
an700=1; D、cos300<cos600;
查看答案和解析>>
科目:初中数学 来源: 题型:
三个牧童A,B,C在一块正方形的牧场上看守一群牛,为保证公平合理,他们商量将牧场划分为三块分别看守,划分的原则是:①每个人看守的牧场面积相等;②在每个区域内,各选定一个看守点,并保证在有情况时,他们所需走的最大距离(看守点到本区域内最远处的距离)相等.按照这一原则,他们先设计了一种如图1-49(1)所示的划分方案,把正方形牧场分成三块相等的矩形,大家分头守在这三个矩形的中心(对角线交点),看守自己的一块牧场.过了一段时间,牧童B和牧童C又分别提出了新的 划分方案.牧童B的划分方案如图1-49(2)所示,三块矩形的面积相等,牧童的位置在三个小矩形的中心.牧童C的划分方案如图1-49(3)所示,把正方形的牧场分成三块矩形,牧童的位置在三个小矩形的中心,并保证在有情况时三个要所需走的最大距离相等.
划分方案.牧童B的划分方案如图1-49(2)所示,三块矩形的面积相等,牧童的位置在三个小矩形的中心.牧童C的划分方案如图1-49(3)所示,把正方形的牧场分成三块矩形,牧童的位置在三个小矩形的中心,并保证在有情况时三个要所需走的最大距离相等.

(1)牧童B的划分方案中,牧童 (填“A”“B”或“C”)在有情况时所需走的最大距离较远.
(2)牧童C的划分方案是否符合他们商量的划分原则?为什么?(提示:在计算
时可取正方形边长为2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com