
三个牧童A,B,C在一块正方形的牧场上看守一群牛,为保证公平合理,他们商量将牧场划分为三块分别看守,划分的原则是:①每个人看守的牧场面积相等;②在每个区域内,各选定一个看守点,并保证在有情况时,他们所需走的最大距离(看守点到本区域内最远处的距离)相等.按照这一原则,他们先设计了一种如图1-49(1)所示的划分方案,把正方形牧场分成三块相等的矩形,大家分头守在这三个矩形的中心(对角线交点),看守自己的一块牧场.过了一段时间,牧童B和牧童C又分别提出了新的 划分方案.牧童B的划分方案如图1-49(2)所示,三块矩形的面积相等,牧童的位置在三个小矩形的中心.牧童C的划分方案如图1-49(3)所示,把正方形的牧场分成三块矩形,牧童的位置在三个小矩形的中心,并保证在有情况时三个要所需走的最大距离相等.
划分方案.牧童B的划分方案如图1-49(2)所示,三块矩形的面积相等,牧童的位置在三个小矩形的中心.牧童C的划分方案如图1-49(3)所示,把正方形的牧场分成三块矩形,牧童的位置在三个小矩形的中心,并保证在有情况时三个要所需走的最大距离相等.

(1)牧童B的划分方案中,牧童 (填“A”“B”或“C”)在有情况时所需走的最大距离较远.
(2)牧童C的划分方案是否符合他们商量的划分原则?为什么?(提示:在计算
时可取正方形边长为2)
解:(1)C [提示:认真观察,用圆规或直尺进行比较,此方法
适用于标准作图.] (2)牧童C的划分方案不符合他们商量的.
划分原则.理山如下:如图1-52所示,在正方形DEFG中,四边
形HENM,MNFP,DHPG都是矩形,且HN=NP=HG,则EN=NF, S矩形HENM=S矩形MNFP,取 正方形边长为2.设HD=x,
正方形边长为2.设HD=x,
则HE=2一x,在 Rt△HEN和Rt△DHG中,由HN=HG,得
EH2+EN2=DH2+DG2,即(2一x)2+l2=x2+22,解得x =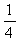 ,∴HE=2- x =
,∴HE=2- x =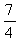 ,
,
∴S矩形HENM=S矩形MNFP=1×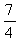 =
=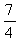 ,∴S矩形DHPG≠S矩形HEMN
,∴S矩形DHPG≠S矩形HEMN
∴牧童C的划分方案不符合他们商量的原则.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
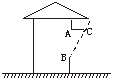
如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8 m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为 ( )
A、1.8tan80°m B、1.8cos80°m C、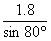 m D、
m D、 m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
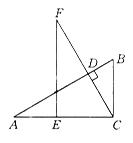
如图1-29所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上.CE =BC,过点E作AC的垂线,交CD的延长线于点F,求证AB=FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
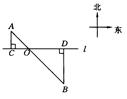
如图1-81所示,A,B是公路l(l为东西走向)两旁的两个村庄,A村到公路l的距离AC=1 km,B村到公路l的距离BD=2 km,B村在A村的南偏东45°方向上.
(1)求A,B两村之间的距离;
(2)为方便村民出行,计划在公路边新建一个公共汽车站P,要求该站到两村的距离相等,请用尺规在图中作出点P的位置.(保 留清晰的作图痕迹,并简要写明作法)
留清晰的作图痕迹,并简要写明作法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com